For this task you need the following basic knowledge: Flächeninhalt eines Dreiecks
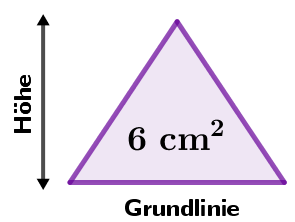
a) Du weißt aus der Angabe, dass der Flächeninhalt des Dreiecks beträgt. Außerdem kannst du den Flächeninhalt eines Dreiecks mit folgender Formel bestimmen: .
Du kannst nun den Wert für den Flächeninhalt einsetzen und so umformen, dass du auf der einen Seite nur noch die Grundlinie und die zugehörige Höhe stehen hast.
Mit Hilfe dieser Umformung musst du also natürliche Zahlen für die Länge der Grundlinie (x in cm) und Höhe (y in cm) finden, sodass sie multipliziert 12 ergeben. Dann hast du Zahlenpaare gefunden, die ein Dreieck mit dem Flächeninhalt von ergeben. Es gibt 6 solcher Paare.
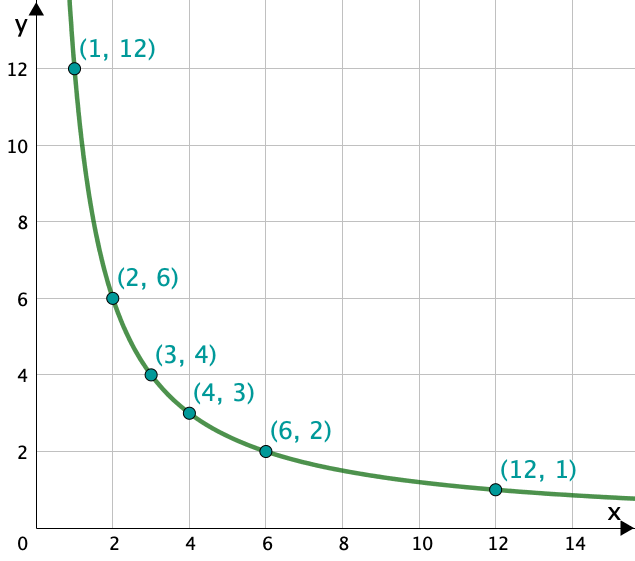
b) Mithilfe der Tabelle der Teilaufgabe a) kannst du diese Aufgabe lösen. Dazu betrachtet man die Tabelle als eine Wertetabelle und die Seitenpaare als Punkte mit einem x und einem y- Wert. Nun kannst du die Punkte in einem Koordinatensystem eintragen und erhältst folgende graphische Darstellung:
Dieser Graph entspricht einer Hyperbel. Die Punkte darf man verbinden, weil jeder (positive) reelle Wert für die Grundseite und die Höhe zulässig sind und nicht nur die ganzzahligen Paare.
Du kannst nun für den Flächeninhalt den Wert aus der Angabe einsetzen und und durch und ersetzen.
Jetzt kannst du die Gleichung nach y auflösen und erhältst den zugehörigen Funktionsterm:
| | | |
| | | |
| | | |
Der Zusammenhang zwischen der Grundlinie (x in cm) und der zugehörigen Höhe (y in cm) eines Dreiecks mit einem Flächeninhalt von wird mit folgender Funktion beschrieben: