Period (of a function)

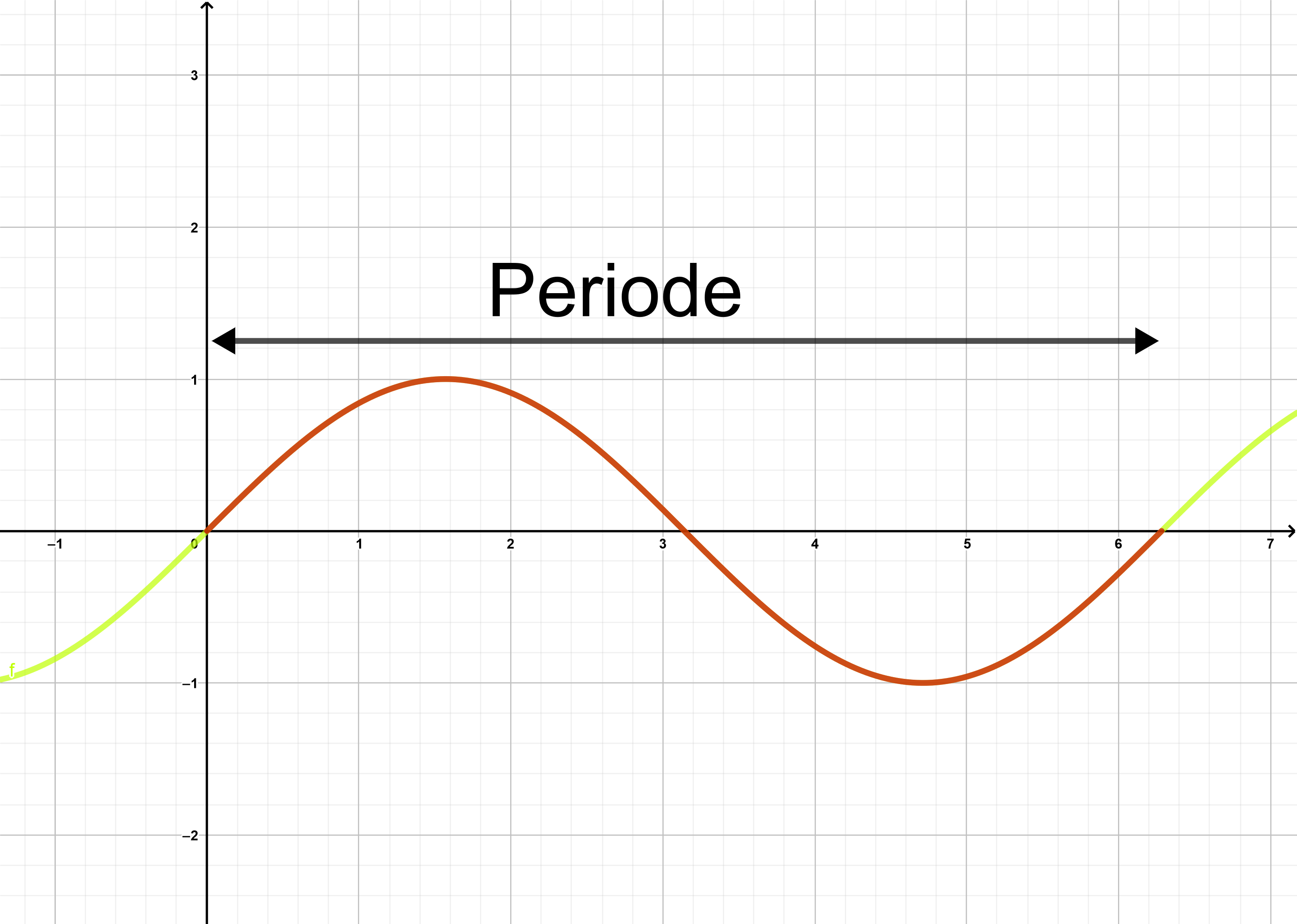
Beispiel

Ein Beispiel einer periodischen Funktion ist die Sinusfunktion.

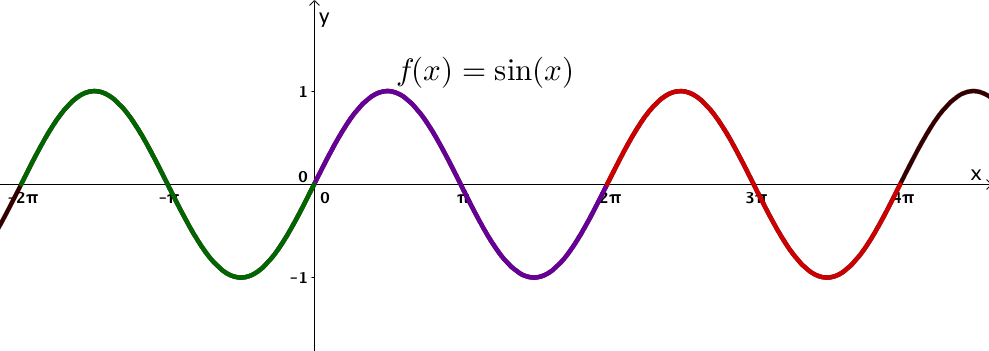
An dem Graphen erkennt man (auch anhand der Farben), dass sich $\sin (x)\backslash sin(x)$ im Abstand von $2\pi 2\backslash mathrm\backslash pi$ wiederholt. Das heißt, die Sinusfunktion besitzt die Periode $2\pi 2\; \backslash pi$.

Startet man an einer beliebigen Stelle $xx$, kann man beliebig oft $2\pi 2\backslash pi$ addieren/subtrahieren und der Funktionswert des Sinus bleibt derselbe. Zum Beispiel:

$\sin (0)=\sin (4\pi )=\sin (-2\pi )\backslash sin(0)=\backslash sin(4\backslash pi)=\backslash sin(-2\backslash pi)$

$\sin (1)=\sin (1+2\pi )=\sin (1+24\pi )\backslash sin(1)=\backslash sin(1+2\backslash pi)=\backslash sin(1+24\backslash pi)$

Das selbe gilt auch für die Kosinusfunktion.

Formel

Falls eine Funktion $ff$ die Periode $pp$ besitzt, dann gilt

$f\left(x\right)=f(x+p)=f(x+2p)=f(x+3p)=\dots f\backslash left(\; x\backslash right)=\; f\backslash left(\; x+\; p\backslash right)=\; f\backslash left(\; x+2\; p\backslash right)=f\; (x+3p)=~\dots$

und $f(x)=f(x-p)=f(x-2p)=f(x-3p)=\dots ~f(x)=f(x-p)=f(x-2p)=f(x-3p)=~\dots$

Hieran erkennt man, dass man zu jedem $xx$ ein Vielfaches der Periode $pp$ addieren/subtrahieren kann und der Funktionswert bleibt dabei derselbe.

Eigenschaften

• Die verschobenen und gestreckten Sinus- und Kosinusfunktionen können durch $a\cdot \sin (b\cdot (x+c))+da\; \backslash cdot\; \backslash sin\backslash left(b\backslash cdot\; (x+c)\backslash right)+d$ und $a\cdot \cos (b\cdot (x+c))+da\; \backslash cdot\; \backslash cos\backslash left(b\backslash cdot\; (x+c)\backslash right)+d$ dargestellt werden. Sie besitzen jeweils die Periode $p=\frac{2\pi }{\mathrm{\mid }b\mathrm{\mid }}p=\backslash frac\{2\backslash pi\}\{|b|\}$.

• Eine Funktion mit Periode $pp$ wiederholt sich ebenfalls auch alle $2p,3p,\dots 2p,\; 3p\; ,\backslash dots$. Als Periode bezeichnet man aber den kleinsten Wert mit dieser Eigenschaft.

• Besitzt eine Funktion die Periode $pp$, dann spricht man davon, dass die Funktion $pp$-periodisch ist.  

• Man sagt, der Graph einer periodischen Funktion ist verschiebungssymmetrisch mit ihrer Periode.

• Addiert man zwei Funktionen mit verschiedenen Perioden, dann ist das kleinste gemeinsame Vielfache der beiden Perioden die Periode der neuen Funktion.

• Den Kehrwert der Periode, also $\frac{1}{p}\backslash frac1\{\; p\}$, nennt man auch Frequenz.