Relations between trigonometric functions

Sine, cosine and tangent have different relationships. A distinction is made between the complement relationship and the supplement relationship.

Komplementbeziehungen

$\sin (90^{\circ} - α) = \cos (α)$
$\cos (90^{\circ} - α) = \sin (α)$
$\tan (90^{\circ} - α) = \frac{1}{\tan (α)}$

Da in einem Dreieck die Summe der Innenwinkel immer 180° ist, gilt in einem rechtwinkligen Dreieck $β = 90 ° - α$ .

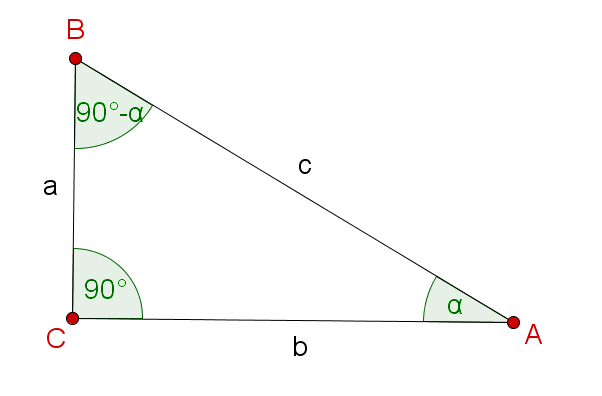
Anhand der Sinus-, Kosinus- und Tangensformeln sieht man:

\sin (90 ° - α) = \frac{Gegenkathete}{Hypotenuse} = \frac{b}{c}

\cos (α) = \frac{Ankathete}{Hypotenuse} = \frac{b}{c} .

Deshalb ist $\sin (90 ° - α) = \cos (α)$ .

Die anderen Gleichungen lassen sich auf gleiche Weise erklären.

Beispiel

Betrachte das gegebene Dreieck. Berechne $\cos (α)$ auf die gleiche Weise wie oben.

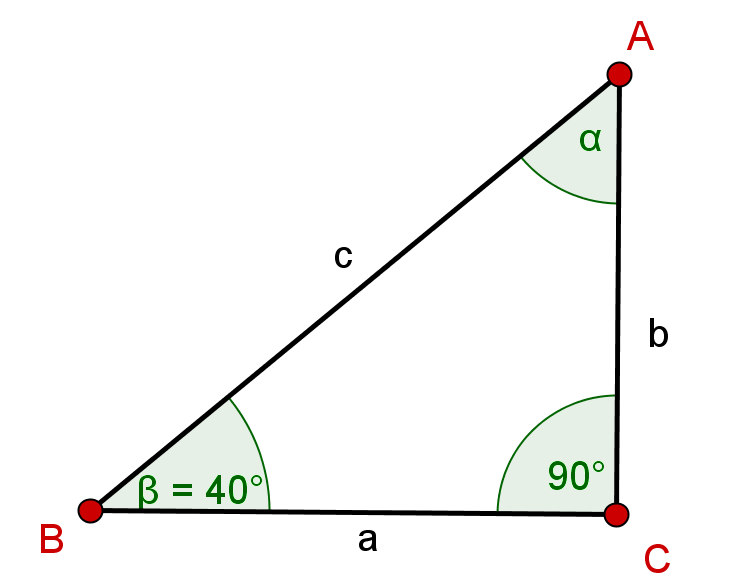
Mit der Komplementbeziehung kannst du $\cos (α)$ mit $\sin (90 ° - α)$ gleichsetzen.

\cos (α) = \sin (90 ° - α)

Wegen der Summe der Innenwinkel gilt folgende Gleichung.

\sin (90 ° - α) = \sin (β)

Füge den Wert von $β$ ein, berechne das Ergebnis und runde es auf $2$ Dezimalstellen.

$\sin (β) = \sin (40 °) \approx 0,59.$

Deshalb ist $\cos (α) \approx 0,59.$

Supplementbeziehungen

Sinus	Kosinus	Tangens
$\sin (180 ° + α) = - \sin (α)$	$\cos (180^{\circ} + α) = - \cos (α)$	$\tan (180^{\circ} + α) = + \tan (α)$
$\sin (180 ° - α) = + \sin (α)$	$\cos (180 ° - α) = - \cos (α)$	$\tan (180^{\circ} - α) = - \tan (α)$
$\sin (360^{\circ} - α) = - \sin (α)$	$\cos (360^{\circ} - α) = + \cos (α)$	$\tan (360^{\circ} - α) = - \tan (α)$

Veranschaulichung

$\sin (180 ° + α) = - \sin (α)$ und $\cos (180 ° + α) = - \cos (α)$ lassen sich hier testen:

By clicking on image or button above you agree that external content from GeoGebra will be loaded. Also personal data may be transferred to this service in accordance with our privacy policy.

Still want more?

You can find more content on this topic here:

Articles

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org