Why is the cosine the derivative of the sine?

The derivative of the sine function can be formally calculated using the $h$ -method. This can be used to show that the derivative is the cosine function.

In school, this relationship is often shown by graphical differentiation.

Finally, this relationship can also be visualised by looking at the respective power series.

Beweis durch die h-Methode

(\sin (x))^{'} = \lim_{h \to 0} \frac{\sin (x + h) - \sin (x)}{h}

Im nächsten Schritt verwendet man das Additionstheorem für die Sinusfunktion:

$\sin (x + y) = \sin (x) \cos (y) + \cos (x) \sin (y)$

(\sin (x))^{'} = \lim_{h \to 0} \frac{\sin (x) \cos (h) + \cos (x) \sin (h) - \sin (x)}{h}

Im Zähler fasst man $\sin (x) \cos (h)$ und $- \sin (x)$ zusammen und klammert $\sin (x)$ aus.

(\sin (x))^{'} = \lim_{h \to 0} \frac{\sin (x) (\cos (h) - 1) + \cos (x) \sin (h)}{h}

Man kann den Bruch in eine Summe aus zwei Brüchen auftrennen.

(\sin (x))^{'} = \lim_{h \to 0} (\frac{\sin (x) (\cos (h) - 1)}{h} + \frac{\cos (x) \sin (h)}{h})

Wenn es die Grenzwerte beider Summanden gibt, kann man den Limes in beide Summanden ziehen.

(\sin (x))^{'} = \lim_{h \to 0} \frac{\sin (x) (\cos (h) - 1)}{h} + \lim_{h \to 0} \frac{\cos (x) \sin (h)}{h}

$\sin (x)$ und $\cos (x)$ hängen nicht von $h$ ab. Deswegen darf man sie vor den Limes schreiben.

(\sin (x))^{'} = \sin (x) \cdot \lim_{h \to 0} \frac{\cos (h) - 1}{h} + \cos (x) \cdot \lim_{h \to 0} \frac{\sin (h)}{h}

$\lim_{h \to 0} \frac{\cos (h) - 1}{h}$ ist die Ableitung des Kosinus an der Stelle $0$ . Das sieht man mit der $h$ -Methode:

$(\cos (0))^{'} = \lim_{h \to 0} \frac{\cos (0 + h) - \cos (0)}{h} = \lim_{h \to 0} \frac{\cos (h) - 1}{h}$ .

(\sin (x))^{'} = \sin (x) (\cos (0))^{'} + \cos (x) \cdot \lim_{h \to 0} \frac{\sin (h)}{h}

Die Ableitung an der Stelle $0$ ist anschaulich die Steigung der Tangente:

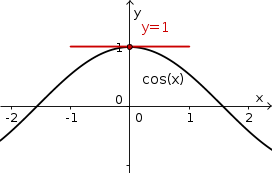
Der Kosinus hat bei $0$ ein Maximum. Deswegen hat die Tangente die Steigung $0$ . Das heißt: $(\cos (0))^{'} = 0$ .

(\sin (x))^{'} = \sin (x) \cdot 0 + \cos (x) \cdot \lim_{h \to 0} \frac{\sin (h)}{h}

= \cos (x) \cdot \lim_{h \to 0} \frac{\sin (h)}{h}

Für sehr kleine $h$ ist $h$ in etwa genauso groß wie $\sin (h)$ .

Im Grenzwert gilt also $\lim_{h \to 0} \frac{\sin (h)}{h} = 1.$

(\sin (x))^{'} = \cos (x) \cdot 1 = \cos (x)

Die Ableitung der Kosinusfunktion

Kennt man bereits die Ableitung der Sinusfunktion, kann man $(\cos (x))^{'}$ mit der Kettenregel ausrechnen. Verschiebt man den Graphen der Sinusfunktion um $\frac{π}{2}$ nach links, erhält man die Kosinusfunktion. Das bedeutet: $\cos (x) = \sin (x + \frac{π}{2})$ . Leitet man beide Seiten der Gleichung ab, erhält man:

(\cos (x))^{'} = {(\sin (x + \frac{π}{2}))}^{'}

Um die Kettenregel zu verwenden, setzt man $v (x) = x + \frac{π}{2}$ und $u (v) = \sin (v)$ . Die Kettenregel lautet:

$u (v (x))^{'} = u^{'} (v (x)) \cdot v^{'} (x)$ .

Da jetzt die Ableitung vom Sinus bekannt ist, kann man $u^{'}$ berechnen.

$u^{'} (v) = \sin^{'} (v) = \cos (v)$ .

Die Ableitung von $v$ ist

$v^{'} (x) = (x + \frac{π}{2}) = 1$ .

u (v (x))^{'} = u (v (x))^{'} = u^{'} (v (x)) \cdot v^{'} (x)

\Rightarrow (\cos (x))^{'} = \cos (x + \frac{π}{2}) \cdot 1

Verschiebt man die Kosinuskurve um $\frac{π}{2}$ nach links, bekommt man die negative Sinuskurve.

(\cos (x))^{'} = - \sin (x)

Mit dieser Rechnung hat man gezeigt: $(\cos (x))^{'} = - \sin (x)$ .

Betrachtung der Potenzreihen

Die Sinus- und Kosinusfunktion können als Potenzreihen dargestellt werden:

$\sin (x) = \sum_{k = 0}^{\infty} (- 1)^{k} \cdot \frac{x^{2 k + 1}}{(2 k + 1)!} = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + . . .$

$\cos (x) = \sum_{k = 0}^{\infty} (- 1)^{k + 1} \cdot \frac{x^{2 k}}{(2 k)!} = 1 - \frac{x^{2}}{2} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + . . .$

Das Ableiten der Sinusfunktion kann durch das Ableiten der Potenzreihe realisiert werden, wobei jeder Summand einzeln nach der Potenzregel abgeleitet werden. Dadurch wird die Potenz kleiner und der Nenner wird mit dem neuen Faktor verrechnet, was hier mit einem Summanden aus der Sinusreihe ersichtlich wird:

\frac{x^{5}}{5!} \overset{a b g e l e i t e t}{⟼} \frac{5 \cdot x^{4}}{5!} = \frac{x^{4}}{4!}

Es entsteht genau der Summand, der in der Potenzreihe des Kosinus auftritt.

Still want more?

You can find more content on this topic here:

Articles

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org