Linear system with two variables

A linear system of equations is composed of several linear equations with common unknowns (variables), all of which are to be satisfied.

Graphical solution

To solve the system of equations graphically, you can resolve the individual lines for $yy$ and draw the corresponding lines into a coordinate system. Then you only need to read off the coordinates of the intersection of the two lines.

The intersection point is at $x=0x=0$ and $y=1y=1$. Thus the solution set is $L=\left\{\left(0\mid 1\right)\right\}L=\backslash left\backslash \{\backslash left(0\backslash left|\backslash ;1\backslash right.\backslash right)\backslash right\backslash \}$.

Solution by computation

In this case, the elimination by equating coefficients is a good choice, since you have already solved both equations for $yy$ in order to solve them graphically.

Set $\mathrm{I}\backslash mathrm\{I\}$ and $\mathrm{I}\mathrm{I}\backslash mathrm\{II\}$ equal and solve for $xx$.

Plug the obtained value for $xx$ into one of the equations, e.g. $\mathrm{I}\mathrm{I}\backslash mathrm\{II\}$.

$y=0+1=1y=0+1=1$

Now, you can write down the solution set.

$L=\left\{\left(0\mid 1\right)\right\}L=\backslash left\backslash \{\backslash left(0\backslash left|1\backslash right.\backslash right)\backslash right\backslash \}$

Linear system with two variables

A linear system of equations is composed of several linear equations with common unknowns (variables), all of which are to be satisfied.

Graphical solution

To solve the system of equations graphically, you can resolve the individual lines for $yy$ and draw the corresponding lines into a coordinate system. Then you only need to read off the coordinates of the intersection of the two lines.

The intersection is at $x\approx 0.71x\backslash approx0.71$ and $y\approx -0.29y\backslash approx-0.29$. Thus the solution set is $L=\left\{\left(0.71\mid -0.29\right)\right\}L=\backslash left\backslash \{\backslash left(0\{.\}71\backslash left|\backslash ;-0\{.\}29\backslash right.\backslash right)\backslash right\backslash \}$.

Solution by computation

In this case, the elimination by equating coefficients is a good choice, since you have already solved both equations for $yy$ in order to solve them graphically.

Set $\mathrm{I}\backslash mathrm\{I\}$ and $\mathrm{I}\mathrm{I}\backslash mathrm\{II\}$ equal and solve for $xx$.

Plug the obtained value for $xx$ into one of the equations, e.g. $\mathrm{I}\mathrm{I}\backslash mathrm\{II\}$.

$y=\frac{5}{7}-1=-\frac{2}{7}\approx -0.29y=\backslash frac\{5\}\{7\}-1=-\backslash frac\{2\}\{7\}\backslash approx-0.29$

Now, you can write down the solution set.

$L=\left\{\left({\displaystyle \frac{5}{7}}\mid -{\displaystyle \frac{2}{7}}\right)\right\}L=\backslash left\backslash \{\backslash left(\backslash dfrac57\backslash left|-\backslash dfrac27\backslash right.\backslash right)\backslash right\backslash \}$

Linear system with two variables

A linear system of equations is composed of several linear equations with common unknowns (variables), all of which are to be satisfied.

Graphical solution

To solve the system of equations graphically, you can resolve the individual lines for $yy$ and draw the corresponding lines into a coordinate system. Then you only need to read off the coordinates of the intersection of the two lines.

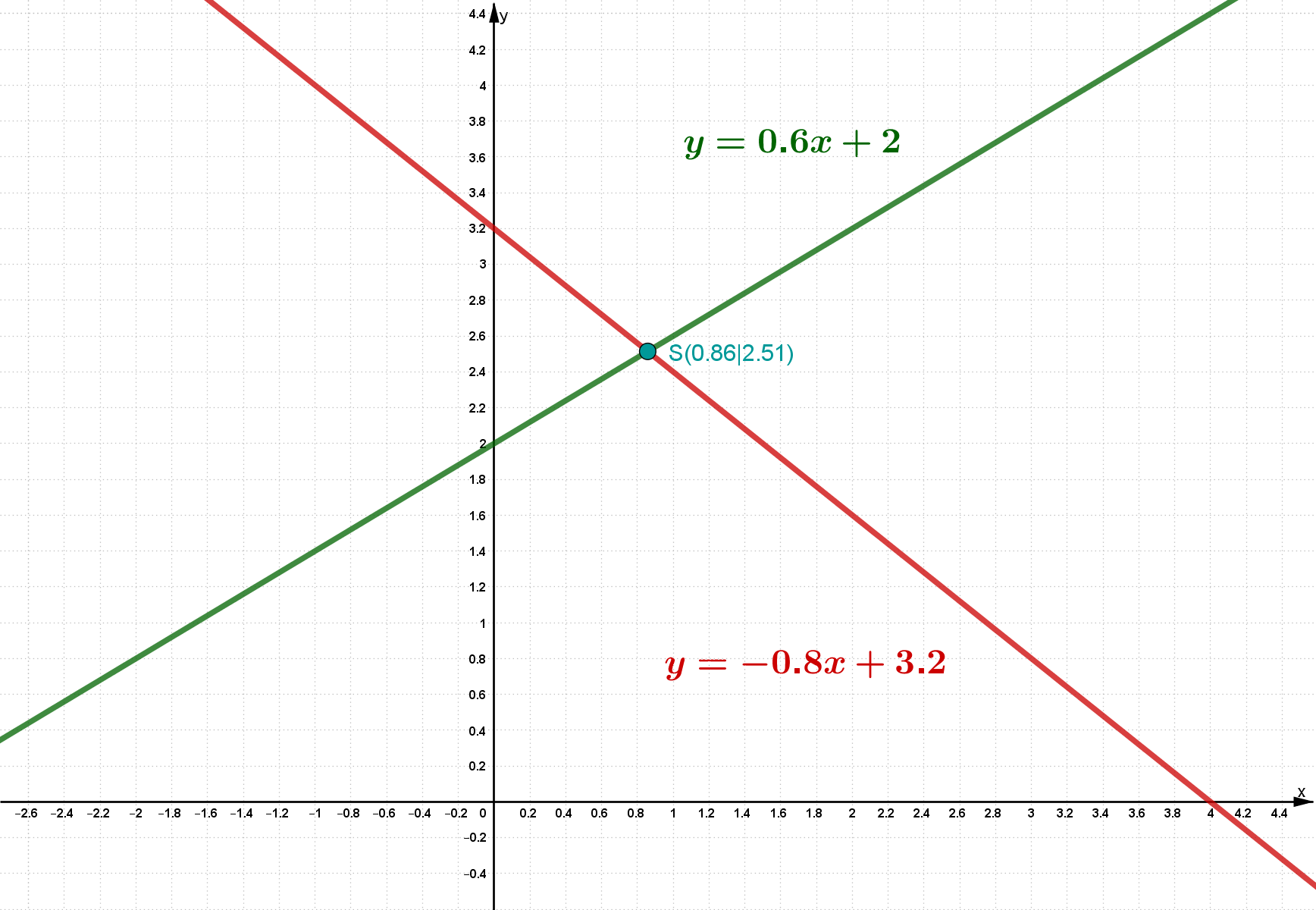
The intersection is at $x\approx 0.86x\backslash approx0\{.\}86$ and $y\approx 2.51y\backslash approx2\{.\}51$. Thus the solution set is $L=\left\{\left(0.86\mid 2.51\right)\right\}L=\backslash left\backslash \{\backslash left(0\{.\}86\backslash left|\backslash ;2\{.\}51\backslash right.\backslash right)\backslash right\backslash \}$.

Solution by computation

In this case, the elimination by equating coefficients is a good choice, since you have already solved both equations for $yy$ in order to solve them graphically.

Set $\mathrm{I}\backslash mathrm\{I\}$ and $\mathrm{I}\mathrm{I}\backslash mathrm\{II\}$ equal and solve for $xx$.

Plug the obtained value for $xx$ into one of the equations, e.g. $\mathrm{I}\backslash mathrm\{I\}$.

$y=0.6\cdot \frac{6}{7}+2=\frac{88}{35}\approx 2.51y=0.6\backslash cdot\backslash frac\{6\}\{7\}+2=\backslash frac\{88\}\{35\}\backslash approx2.51$

Now, you can write down the solution set.

$L=\left\{\left({\displaystyle \frac{6}{7}}\mid {\displaystyle \frac{88}{35}}\right)\right\}L=\backslash left\backslash \{\backslash left(\backslash dfrac67\backslash left|\backslash dfrac\{88\}\{35\}\backslash right.\backslash right)\backslash right\backslash \}$