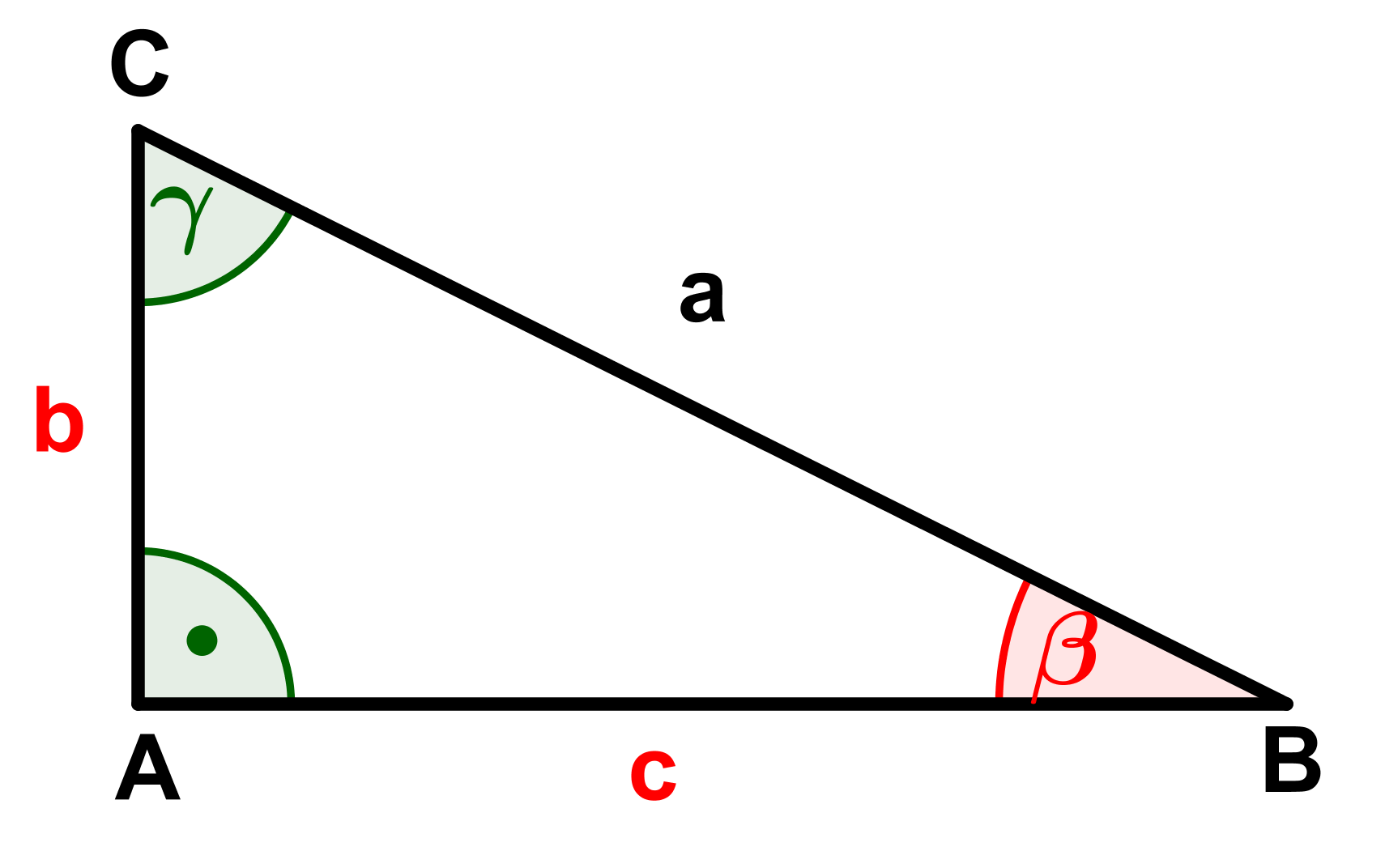
For this task you need the following basic knowledge: Trigonometry on the unit circle
You can calculate by subtracting all given angles from the total sum of all angles in a triangle .
Then you compute using the Pythagorean theorem.
Note in particular that c is not the hypotenuse of the triangle, but (see picture above), so that the Pythagorean form remains similar, but now , and do not take the familiar roles, where , would be the cathetuses and the hypotenuse.