Exercises: Linear functions, zeros, axis intercepts
- 1
Read off the -axis intercept from the graph.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
For this task you need the following basic knowledge: Linear function
The -axis intercept is the -value of the intersection with the -axis , so .
You get the -axis intercept by looking at the intersection of the line with the y-axis.
- 2
Read off the zero from the graph.
For this task you need the following basic knowledge: Calculating zeros
The zero is the -value of the intersection of the line with the -axis , so .
You determine the zero by looking at the intersection of the line with the -axis.
For this task you need the following basic knowledge: Calculating zeros
The zero is the -value of the intersection of the line with the -axis , so .
You determine the zero by looking at the intersection of the line with the -axis.
For this task you need the following basic knowledge: Calculating zeros
The zero is the -value of the intersection of the line with the -axis , so .
You determine the zero by looking at the intersection of the line with the -axis.
For this task you need the following basic knowledge: Calculating zeros
The zero is the -value of the intersection of the line with the -axis , so .
You determine the zero by looking at the intersection of the line with the -axis.
For this task you need the following basic knowledge: Calculating zeros
The zero is the -value of the intersection of the line with the -axis , so .
You determine the zero by looking at the intersection of the line with the -axis.
The zero is the -value of the intersection of the line with the -axis , so .
You determine the zero by looking at the intersection of the line with the -axis.
- 3
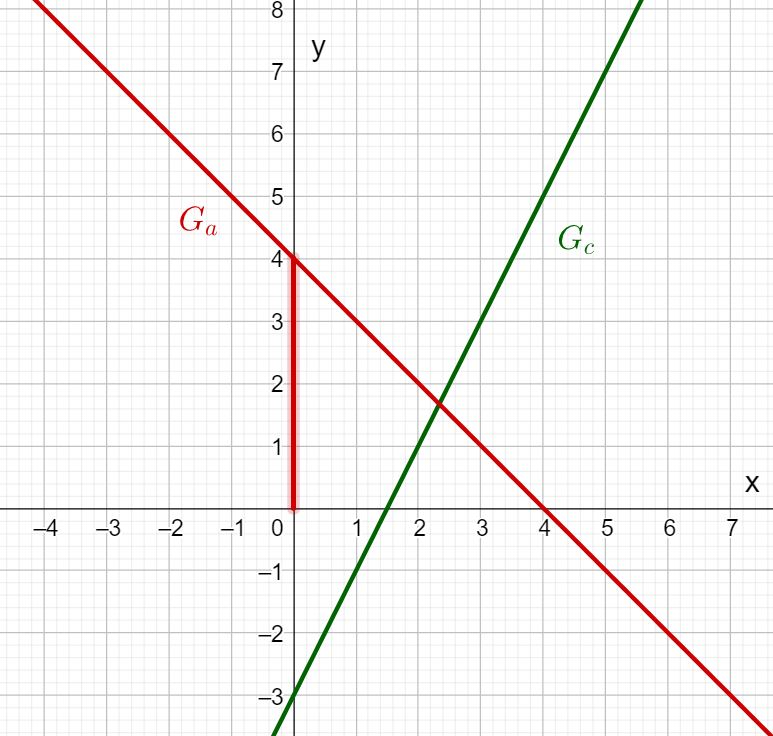
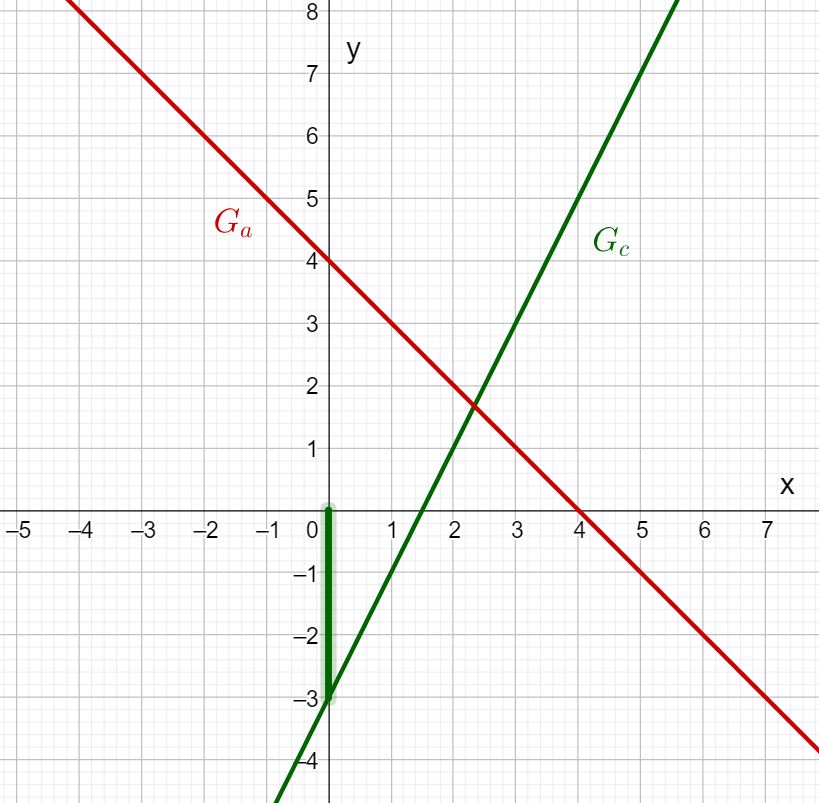
Look at the graphs of the functions and .
Read off the -axis intercept and the slope of the lines and enter them in the boxes!
Can you work out the function term from this?
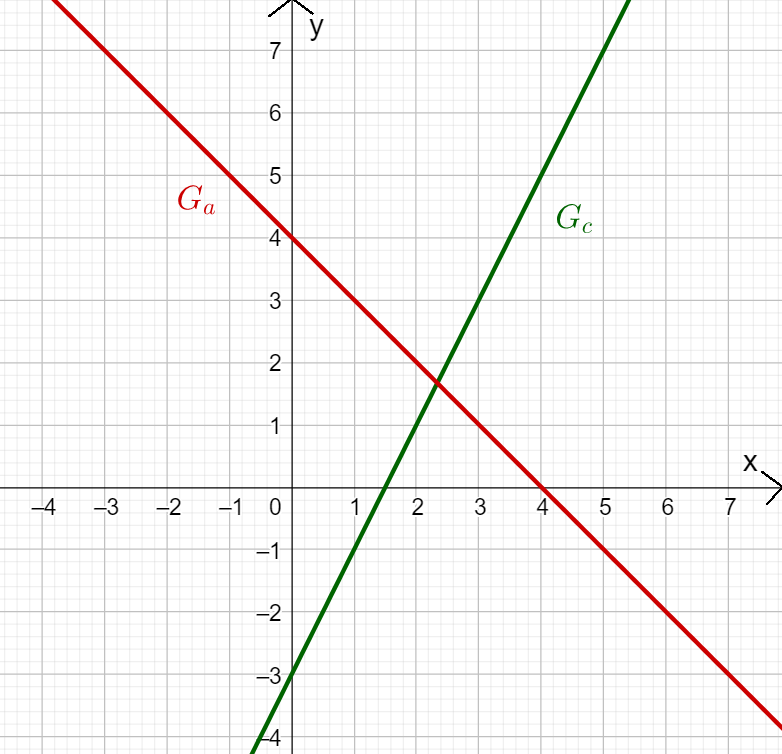
What is the -axis intercept of ?
For this task you need the following basic knowledge: Line equation in analytic geometry
Determining the -axis intercept
You determine the -axis intercept by looking at the intersection of the straight line with the -axis. In this case:
The -axis intercept is the -value of the intersection point , i.e. .
Notice where the straight line intersects the -axis.
Determine the intersection.
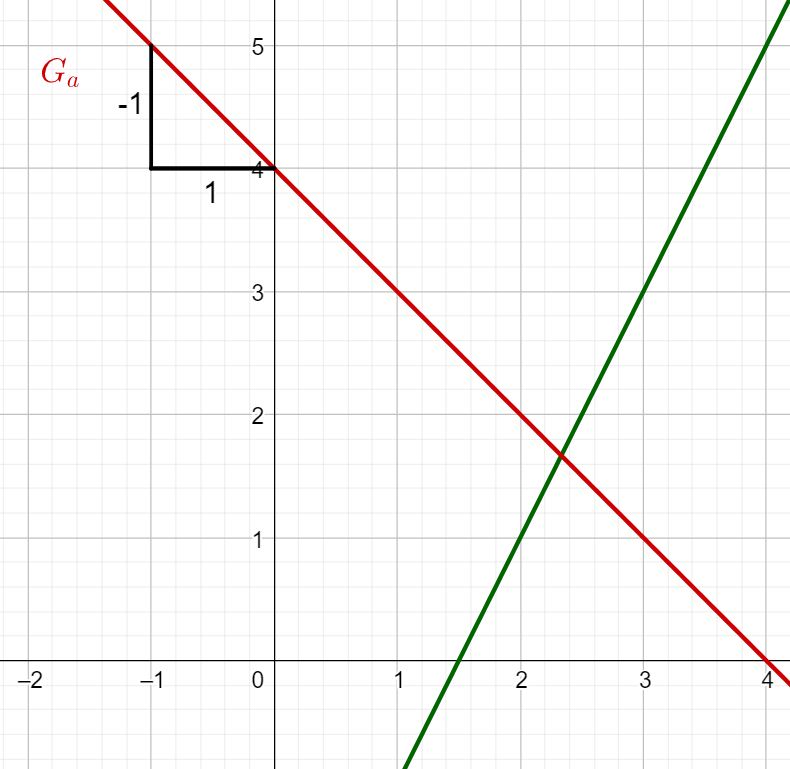
What is the slope of ?
For this task you need the following basic knowledge: Slope/Gradient of a line
Determining the slope
The easiest way to determine the slope of a straight line is to use a gradient triangle.
In the case of :
You have to go one length unit to the right and one length unit down.
Therefore, you get the slope
Pick a gradient triangle (see below).
Then determine the slope.
What is the function term of ?
For this task you need the following basic knowledge: Linear function
Setting up the function term
The function term of a linear function takes the form:
Here is the slope and the -axis intercept.
If you insert the values from the previous sub-tasks, you get:
Simplified, that is:
The function equation of is thus:
.
Recap the basic knowledge about linear functions.
Put your previous values into the function (see below for a more detailed explanation).
What is the y-axis intercept of c(x)?
For this task you need the following basic knowledge: Line equation in analytic geometry
Determining the -axis intercept
You determine the -axis intercept by looking at the intersection of the straight line with the -axis. In this case:
Therefore, the -axis intercept of is .
Notice where the straight line intersects the -axis.
Determine the intersection.
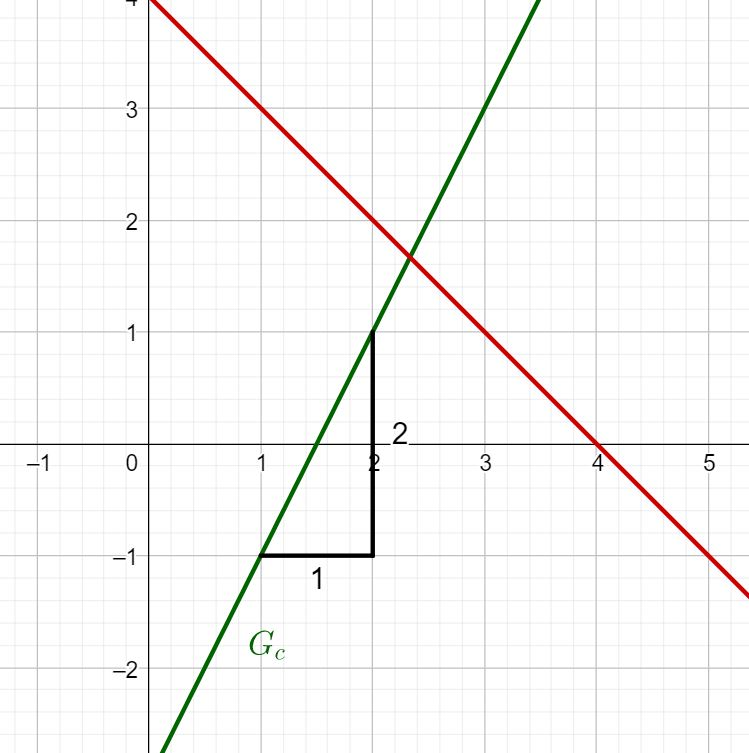
What is the slope of ?
For this task you need the following basic knowledge: Slope/Gradient of a line
Determining the slope
The easiest way to determine the slope of a straight line is to use a gradient triangle.
In the case of :
You have to go one length unit to the right and two length units up.
Therefore, you get the slope:
Pick a gradient triangle (see below).
Then determine the slope.
What is the function term of ?
For this task you need the following basic knowledge: Linear function
Setting up the function term
The function term of a linear function takes the form:
Here is the slope and the -axis intercept.
If you insert the values from the previous sub-tasks, you get:
The functional equation of is thus:
Recap the basic knowledge about linear functions.
Put your previous values into the function (see below for a more detailed explanation).
- 4
Consider the lines and .
Check whether the points , , , and are on either of both lines.
Complete the coordinates so that the points lie on : P , , , .
Show that lies on both lines. What does this mean?
For this task you need the following basic knowledge: Line equation
Part 1
Drawing a sketch
Select any point on the straight line, e.g. the -axis intercepts and . Go from there 1 unit to the right and, corresponding to the slopes, upwards and downwards. Connect the two points to form a straight line.
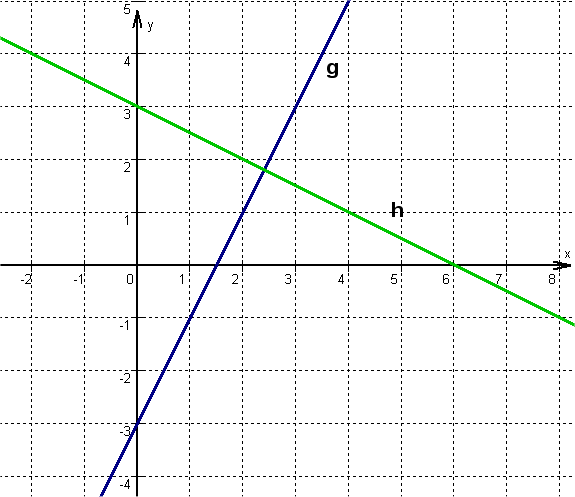
If you look at the straight line and, for example, the position of point , you will see that it will hardly lie on the straight line , but probably on . Similarly, you can decide for other points whether a mathematical check is worthwhile: Point can only lie on , for example.
Check by computation
on
Put the coordinates of the points into the equation in question. So set and .
Check if the equation is a true statement.
Thi is a true statement.
lies on .
does not lie on any of the straight lines. This can be clearly seen in the sketch.
is plugged into : This statement is false, so does not lie on .
is plugged into : This statement is false, so does not lie on .
is plugged into : This statement is true, so lies on .
Part 2
Completing coordinates
;
The given coordinate of the point (the -coordinate) is inserted into the function equation and the missing -coordinate is calculated from it.
Q:
R:
S:
Part 3
Proof for
Insert the coordinates of into both line equations. If the statements are true, lies on the lines.
on :
on :
Both equations give correct statements, so the point lies on both straight lines.
Is the intersection point of the lines.
- 5
Draw the graphs of the following lines including the point of intersection with the -axis and a gradient triangle. Calculate the point of intersection with the -axis and check the result using the graph.
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
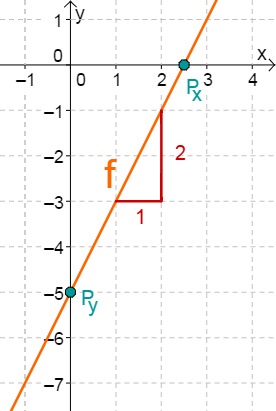
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
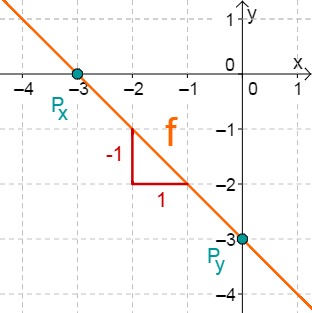
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
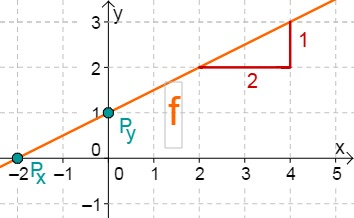
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
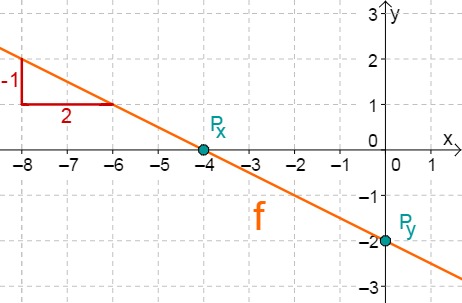
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
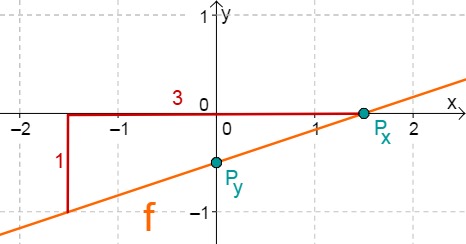
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
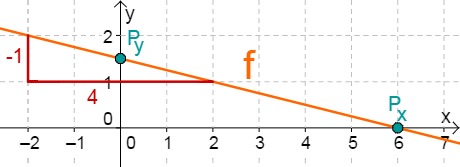
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
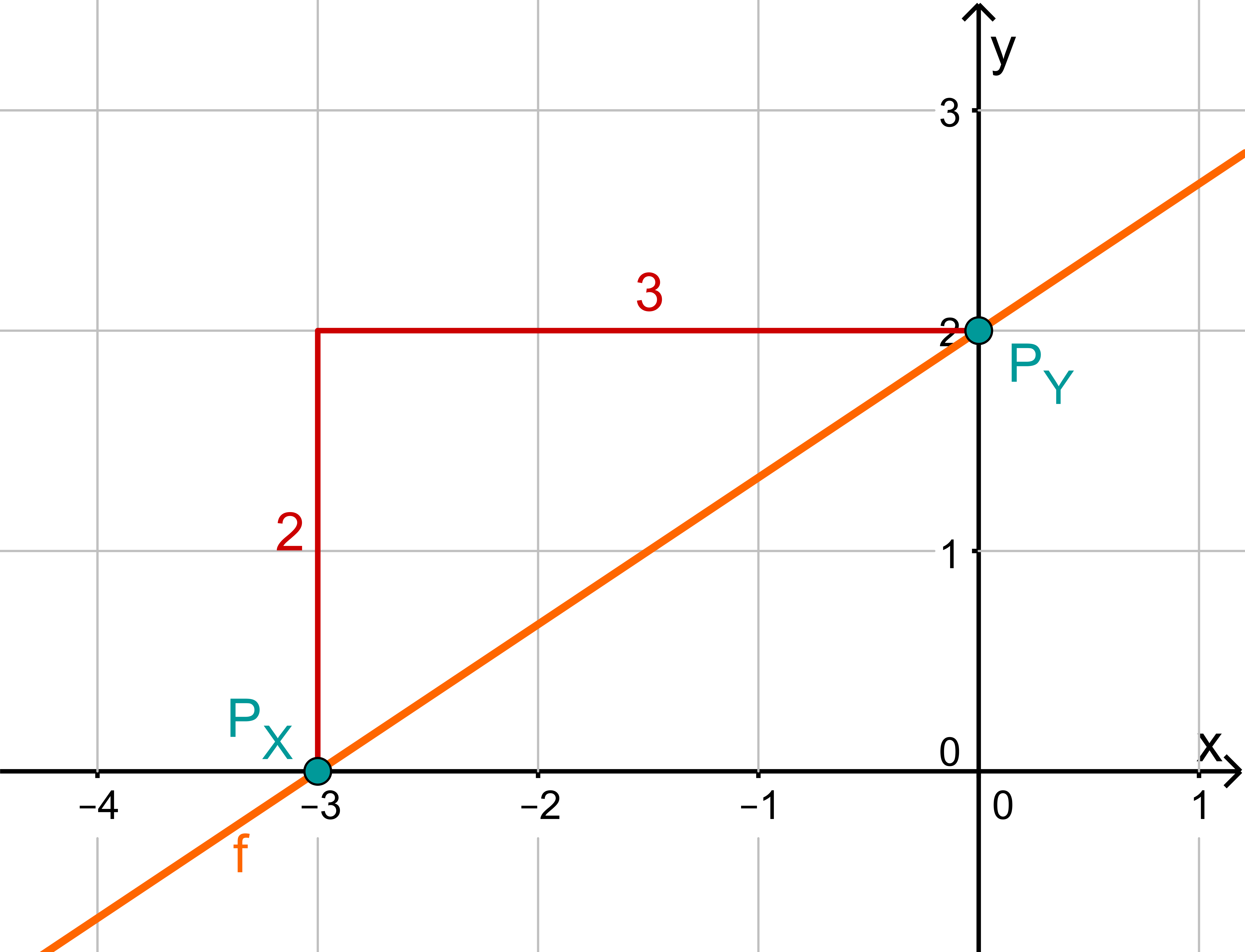
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
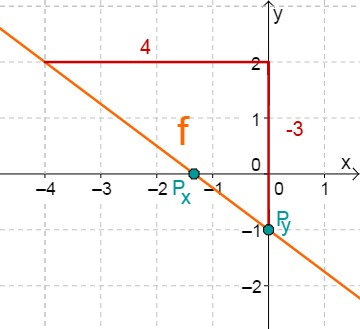
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
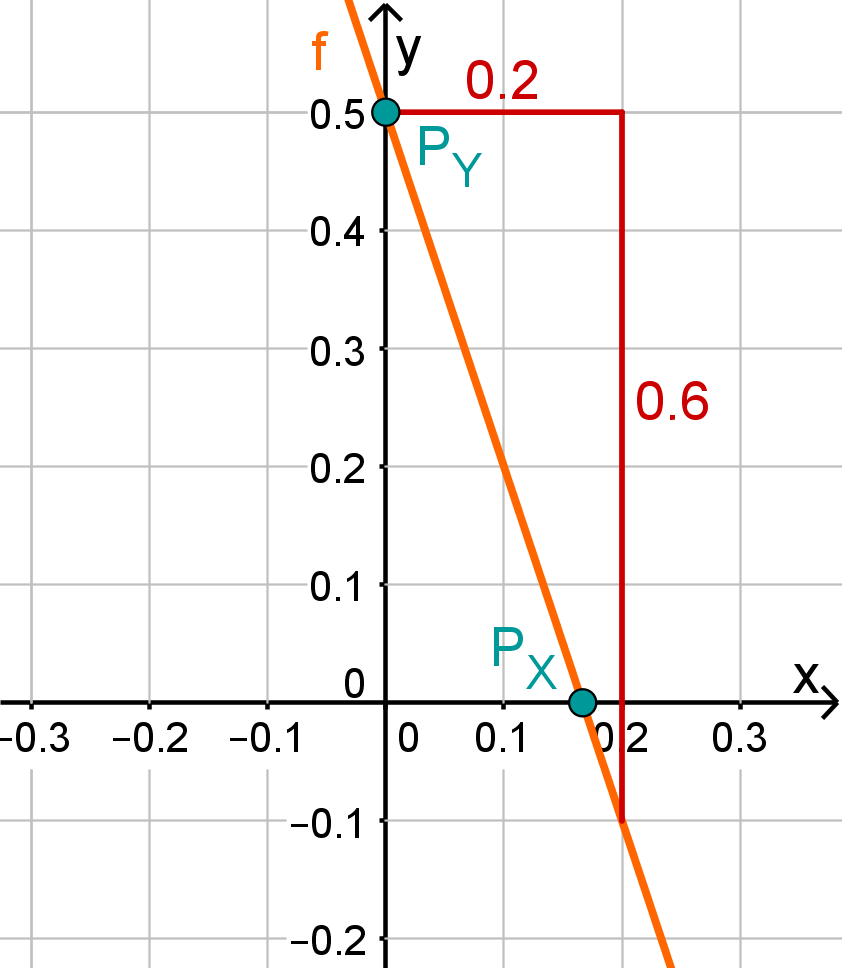
For this task you need the following basic knowledge: Lines in coordinate systems
First read off the -axis intercept and the slope from the function equation.
Calculate the intersection point with the -axis. This is done by setting the function term equal to 0.
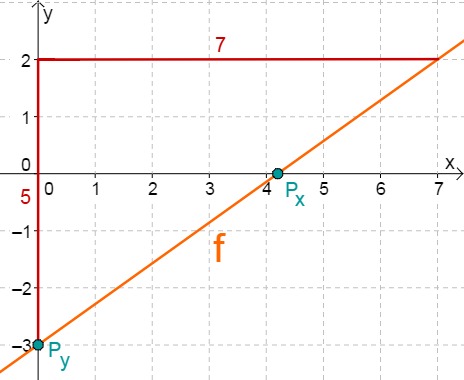
- 6
Draw the lines and into a coordinate system. Determine the zeros and the point of intersection.
For this task you need the following basic knowledge: Linear function
Draw the graphs
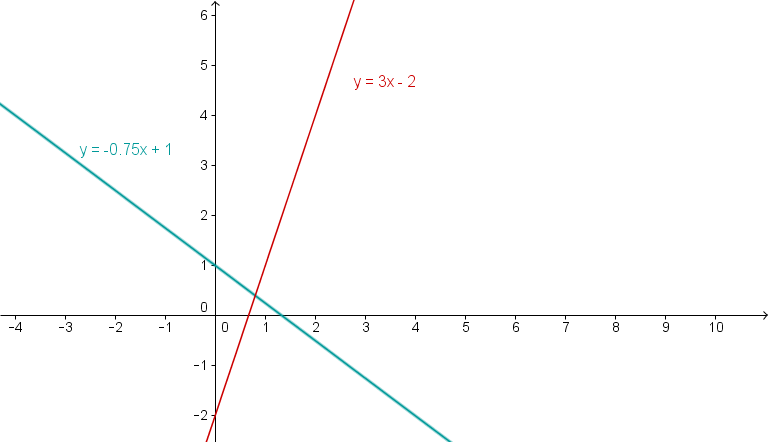
Determining the zeros
Set to determine the zero point. This is the point where the line intersects the -axis.
Proceed in the same way for the second line.
↓ Set y=0 to determine the zero.
↓ You divide by a fraction -> multiply by the reciprocal value
Determining of the intersection point
Set the two function equations equal. The straight lines intersect where both have the same -value at the same -position.
↓ Plug into one of the two functions.
The intersection point is at .
- 7
Determine the intersection points with the coordinate axes of the following straight lines.
Intersection with the -axis
Calculate the intersection of the line with the -axis.
Set the expression for the line equation equal to 0 and solve for .
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
To do this, plug the value into the expression for the straight line equation.
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
Set the expression for the line equation equal to 0 and solve for .
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
To do this, plug the value into the expression for the straight line equation.
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
Set the expression for the line equation equal to 0 and solve for .
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
To do this, plug the value into the expression for the straight line equation.
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
Set the expression for the line equation equal to 0 and solve for .
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
To do this, plug the value into the expression for the straight line equation.
The line intersects the -axis at .
To obtain a general line equation , multiply out the bracket
Intersection with the -axis
Calculate the intersection of the line with the -axis.
Set the expression for the line equation equal to 0 and solve for .
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
To do this, plug the value into the expression for the straight line equation.
The line intersects the -axis at .
Transform the equation
To obtain a general line equation , swap both elements on the right side.
Intersection with the -axis
Calculate the intersection of the line with the -axis.
Set the expression for the line equation equal to 0 and solve for .
The line intersects the -axis at .
Intersection with the -axis
Calculate the intersection of the line with the -axis.
To do this, plug the value into the expression for the straight line equation.
The line intersects the -axis at .
- 8
Set up the function equation for the line through the points and and calculate the intersection of the line with the -axis.
For this task you need the following basic knowledge: Linear function
;
Determine the slope of the general line equation using the difference quotient .
Insert and the coordinates of a point, e.g. , into the general line equation.
Simplify:
↓ solve for
Intersection with the -axis
At the intersection with the -axis the -value is 0.
Solve for . To do this, we use
Note that both summands must be multiplied.
Add 15
The line intersects the -axis at .
- 9
Transform the equation into the form .
↓ The fraction on the right side vanishes because .
↓ Swap the left and right sides.
↓ Note: On the right-hand side, each element is multiplied by :
↓ Multiply out the bracket.
- 10
Two lines and intersect on the -axis in .
Determine possible function terms.
For this task you need the following basic knowledge: Linear function
There are several solutions to this problem. We are looking for two different linear functions that both pass through the point .
A very simple example would be , i.e. the -axis and .
obviously runs through . For this can also be checked very easily: .
Other possible functions are:
, (generally for any ).
Consider the point through which both lines must pass.
Determine two different functions that go through this point.
- 11
Consider the linear function .
Draw the graph and mark the function value .
Draw the graph and mark the function value .
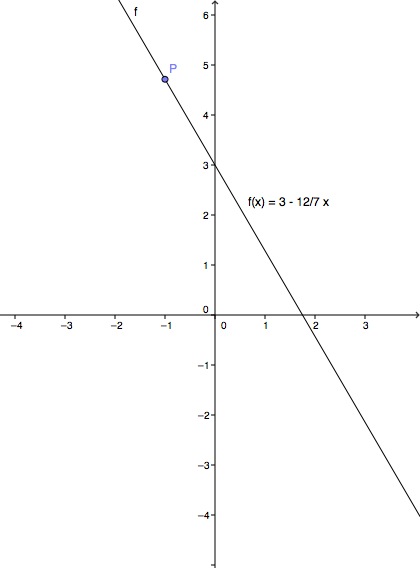
Is the point on the graph of ?
Check whether the point lies on the graph of the function.
To do this, insert the -value into the function equation .
↓ multiply
↓ subtract
Result
The point is not on the graph because the function value of is a non-terminating decimal fraction and not the finite decimal fraction .
If you have calculated with rounded values, you might have mistakenly conclude that the point is on the graph. However, this is not the case.
- 12
Consider the lines and .
Check whether the points , , , and lie on one of the straight lines.
For this task you need the following basic knowledge: Line equation
Checking with sketch
Select any point on the straight line, e.g. the -axis sections and . Go from there 1 to the right and, corresponding to the slopes, upwards or downwards. Connect the two points to form a straight line.

If you look at the course of the straight line and, for example, the position of point , you will see that it will hardly lie on the straight line , but probably on . Similarly, you can decide for other points whether a mathematical check is worthwhile: Point can only lie on , for example.
Computational verification
Plug into :
Plug the coordinates y=-1 and x=1 into the equation.
That is a true statement.
⇒ is on .
does not lie on any of the straight lines. This can be clearly seen in the sketch.
Plug into :
⇒
This statement is false, so is not on .
Plug into :
⇒
This statement is false, so is not on .
Plug into :
This statement is correct, so lies on .
Complete the coordinates so that the points lie on : , , , .
For this task you need the following basic knowledge: Line equation
Complete coordinates
;
The given coordinate of the point (the -coordinate) is inserted into the function equation and the missing -coordinate is calculated from it.
⇒
Q:
R:
S:
Show that lies on both straight lines. What does this mean?
For this task you need the following basic knowledge: Line equation
Proof for
Plug the coordinates of into both line equations. If the statements are true, lies on the lines.
into :
into :
Both equations give correct statements, so the point lies on both lines.
Is the intersection point of the lines.