Exercises: Linear functions as lines in coordinate systems

1
Draw the lines $y = 3 x - 2$ and $y = - \frac{3}{4} x + 1$ into a coordinate system. Determine their zeros and the intersection of both lines.

For this task you need the following basic knowledge: linear function
Drawing the graph
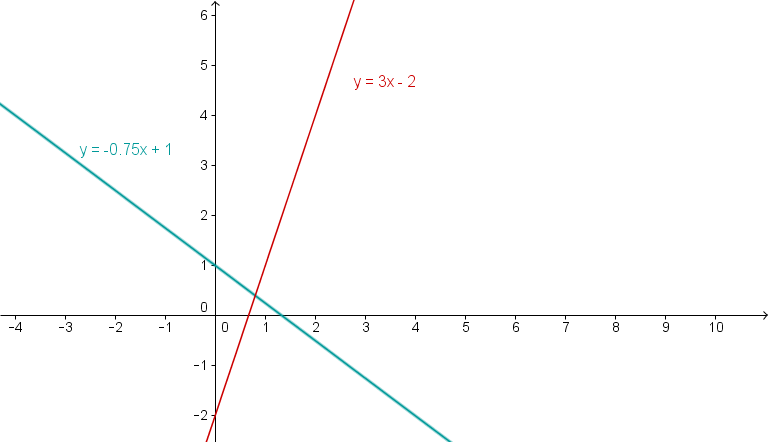
Determining the zeros
$y = 3 x - 2$
Set $y = 0$ to determine the zero. This is, since the line intersects the $x$ -axis exactly where $y = 0$ .
$3 x - 2$ $=$ $0$ $+ 2$
$3 x$ $=$ $2$ $: 3$
$x_{N1}$ $=$ $\frac{2}{3}$
↓
The first line has a zero at $x_{N} = \frac{2}{3}$ .
Proceed in the same way for the second line.
$y$ $=$ $- \frac{3}{4} x + 1$
↓
Set y=0 to determine the zero
$- \frac{3}{4} x + 1$ $=$ $0$ $- 1$
$- \frac{3}{4} x$ $=$ $- 1$ $: (- \frac{3}{4})$
$x$ $=$ $\frac{1}{\frac{3}{4}}$
↓
You divide by a fraction $\to$ multiply by the reciprocal value
$x_{N2}$ $=$ $\frac{4}{3}$
↓
The first line has a zero at $x_{N} = \frac{4}{3}$ .
Determining the interscetion
Set the two function equations equal. The lines intersect where both have the same $x$ - and the same $y$ -value.
$3 x - 2$ $=$ $- \frac{3}{4} x + 1$ $+ \frac{3}{4} x + 2$
$3 x + \frac{3}{4} x$ $=$ $1 + 2$
$3.75 x$ $=$ $3$ $: 3.75$
$x$ $=$ $\frac{3}{3.75}$
$x_{s}$ $=$ $0.8$
↓
Plug $x_{s}$ into one of both functions
$y$ $=$ $3 \cdot 0.8 - 2$
$y$ $=$ $2.4 - 2$
$y_{s}$ $=$ $0.4$
$\Rightarrow S (0.8 | 0,4)$
The intersection is at $S (0.8 | 0.4)$ .
2
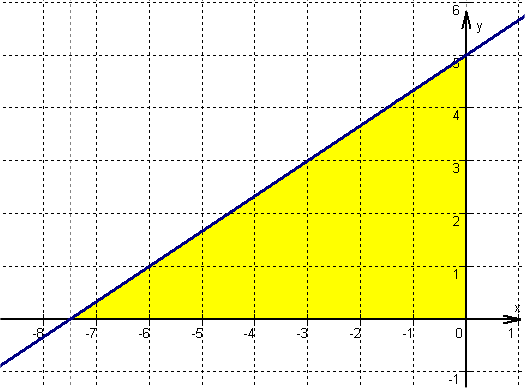
Determine the area of the triangle from the coordinate axes and the straight line $g : y = \frac{2}{3} x + 5$ .
Write your result without area units in the answer box.

For this task you need the following basic knowledge: formula for the area of a triangle
Area of the triangle
Since the coordinate axes are perpendicular to each other, they can be used as the baseline and height of the formula for calculating the area of the triangle.
Determine the height
g: $y = \frac{2}{3} x + 5$
The y-intercept is given as t of the line equation.
The straight line intersects the y-axis in (0|5).
With the x-axis as the baseline, the distance from the point to the origin is the height.
$\Rightarrow$ The height h = $\sqrt{5^{2} - 0^{2}} = 5$
Calculate baseline
To specify the baseline, the point of intersection of the straight line with the x-axis must be calculated. Set y to 0 for this.
$0 = \frac{2}{3} x + 5$
Solve for x. $| - 5$
$\frac{2}{3} x = - 5$
$| : \frac{2}{3}$
$x = - \frac{15}{2} = - 7.5$
The straight line intersects the x-axis in (-7,5|0)
So the distance from this point to the origin is the length of the baseline.
$\Rightarrow$ The length of the baseline g is $\sqrt{(- 7.5)^{2} + 0^{2}} = 7.5$ .
Calculate the area
Substitute the baseline and height into the formula to calculate the area of the triangle.
$\Rightarrow A = \frac{5 \cdot 7,5}{2} = 18.75 AU$
AU stays for "area unit".
Illustration:
3
A straight line that passes through $P (2.5 | 0)$ encloses a triangle with the coordinate axes.
For what slope is this triangle isosceles?

For this task you need the following basic knowledge: Line equation and triangle
Two sides of the triangle are coordinate axes. These have a right angle between them, so the triangle is certainly right-angled.The right angle cannot be a base angle in an isosceles triangle, so the legs of equal length are the catheti (axes).
There are two ways to choose a point so that the legs are of equal length:
$Q_{1} (0 | 2.5)$ and $Q_{2} (0 | - 2.5)$ . The triangle is then in the 1st quadrant or in the 4th quadrant. The triangle cannot be in other quadrants since P is on the boundary between the first and fourth.
This gives you a slope triangle for $Q_{1}$ with slope -1 and one for $Q_{2}$ with slope 1.
Such a triangle thus occurs for the gradients $m_{1} = - 1$ and $m_{2} = 1$ .

Determine for which x-values of $f (x) > 0$ .

$f (x) = 0.4 x + 1$

For this task you need the following basic knowledge: solve inequalities
$f (x)$ $>$ $0$
↓
Insert the function term.
$0.4 x + 1$ $>$ $0$ $- 1$
↓
Sort by x-terms and numbers.
$0.4 x$ $>$ $- 1$ $: 0.4$
↓
Solve for x (observe $0.4 > 0$ , the inequality sign remains).
$x$ $>$ $- \frac{1}{0.4} = - 2.5$
$ f (x)$ is greater than zero for all $x > - 2.5$ .

$f (x) = - 1.5 (x - 2)$

$f (x) = \frac{x}{5} - \frac{7}{5}$

For this task you need the following basic knowledge: solve inequalities.
$f (x)$ $>$ $0$
↓
Insert functional equation.
$\frac{x}{5} - \frac{7}{5}$ $>$ $0$ $+ \frac{7}{5}$
↓
Sort by x-terms and numbers.
$\frac{x}{5}$ $>$ $\frac{7}{5}$ $\cdot 5$
↓
Solve for x (5>0, so no change to the inequality sign)
$x$ $>$ $7$
For $x > 7$ is $f (x)$ positive.

5
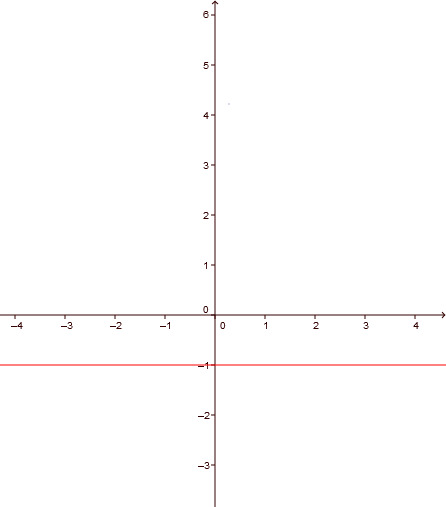
Describe in words the position of the line with the equation:
$y = - 1$

For this task you need the following basic knowledge: Description of line equations
This is a constant function, i.e. the function does not depend on x.Each of the x-values has the y-value -1 . The equation describes a straight line that is parallel to the x-axis and that has 1 below the x-axis.
$\Rightarrow y = - 1$ describes a straight line with a slope of 0 through the point $(0, - 1)$ .
the graph looks like this:

$x + y = - 2$

For this task you need the following basic knowledge: Description of line equations
$y + x = - 2$
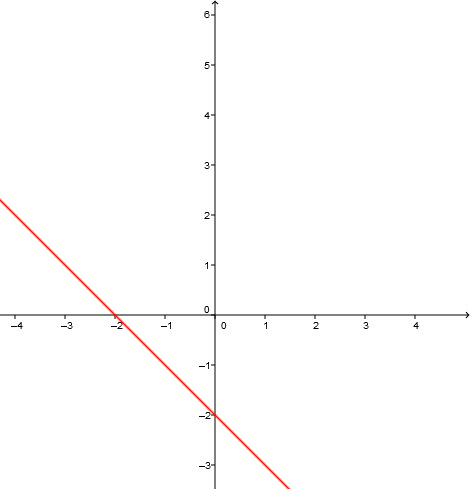
Rewrite so that y is alone on one side of the equals sign.
$y = - x - 2$
Read the slope $m$ and the y-intercept t.
The equation describes a straight line with the slope m=-1 and the y-intercept $t = - 2$ (She goes through the point $(0, - 2)$ ) , i.e. the bisector of the II and IV quadrants shifted down by 2.
The graph looks like this:
6
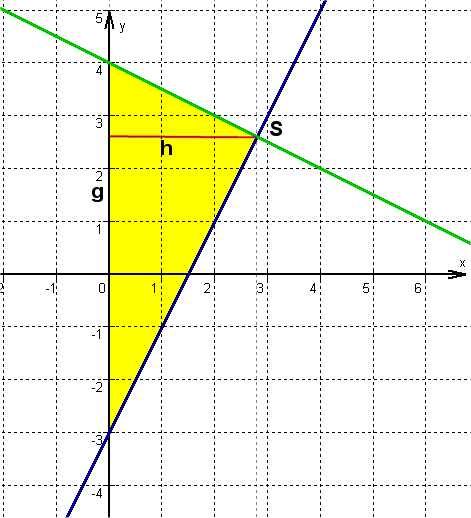
The straight lines are given $g$ : $y = 2 x - 3$ and $h$ : $y = - 0.5 x + 4$ .
Calculate the intersection of the two lines.

g: $y = 2 x - 3$ and h: $y = - 0.5 x + 4$
Equate the lines to get the x-value of the intersection.
$2 x - 3$ $=$ $- 0.5 x + 4$ $+ 0.5 x | + 3$
$2.5 x$ $=$ $7$ $: 2.5$
$x$ $=$ $2.8$
$y$ $=$ $2 \cdot 2.8 - 3$
↓
Note "dot before dash"
$y$ $=$ $5.6 - 3 = 2.6$
The x-value must now be inserted into one of the lines to get the y-value of the point of intersection.
$y$ $=$ $2 \cdot 2.8 - 3$
$y$ $=$ $5.6 - 3$
$y$ $=$ $2.6$
The intersection of the lines: $S (2.8 | 2.6)$

Calculate the area of the triangle formed by g and h and the y-axis.

The base line g of the triangle is 7
Here, starting from the formula for calculating the area of a triangle, the section between the two intersection points of the straight lines with the y-axis is taken as the base line. These intersections are marked with the letter t. For the given straight lines, the range lies between $- 3$ and $4$ $\Rightarrow$ $g = 7$
The height h is 2.8. The height h is always perpendicular to the base line and is therefore parallel to the x-axis. It thus corresponds to the length from the origin to the x-value of the intersection of both straight lines.
$\Rightarrow A = \frac{1}{2} \cdot g \cdot h = \frac{7 \cdot 2.8}{2} = 9.8$
7
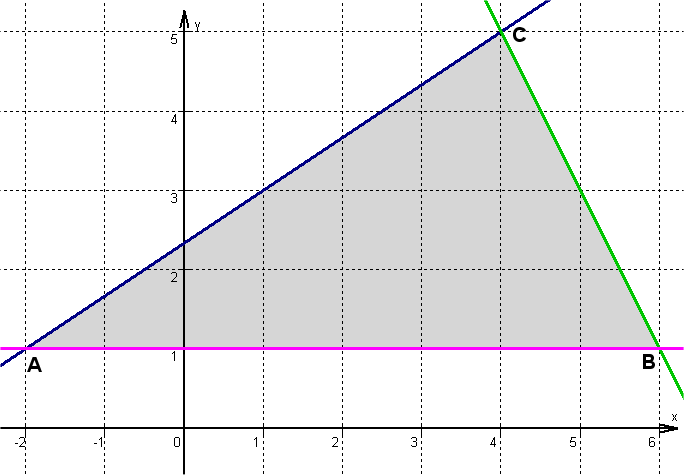
The three points are given $A (- 2 | 1)$ , $B (6 | 1)$ and $C (4 | 5)$ .
Set the equation of the line $A B$ , $A C$ and $B C$ .

For this task you need the following basic knowledge: line equation.
Straight line AB:
$A = (- 2 | 1)$ and $B = (6 | 1)$
Determine the slope m with the difference quotient.
$m = \frac{1 - 1}{- 2 - 6} = \frac{0}{- 8} = 0$
So the straight line is parallel to the x-axis.The y-intercept t is therefore equal to the y-coordinate of the two points.
$t = 1$
Put together the equation of the line.
$y = m x + t = 0 \cdot x + 1 = 1$
Straight line AC:
$A = (- 2 | 1)$ and $C = (4 | 5)$
Determine the slope m with the difference quotient.
$m = \frac{1 - 5}{- 2 - 4} = \frac{- 4}{- 6} = \frac{2}{3}$
So the straight line is parallel to the x-axis.The y-intercept t is therefore equal to the y-coordinate of the two points.
$y = m x + t$
Put a point for example. A .
$1 = \frac{2}{3} (- 2) + t$
Solve for t .
$t = 1 - \frac{- 4}{3} = 1 + \frac{4}{3} = \frac{7}{3}$
Put together the equation of the line.
$y = m x + t = \frac{2}{3} x + \frac{7}{3}$
Straight line BC:
$B = (6 | 1)$ and $C = (4 | 5)$
Determine the slope m with the difference quotient.
$m = \frac{1 - 5}{6 - 4} = \frac{- 4}{2} = - 2$
Set up the equation for the y-intercept.
$y = m x + t$
Put a point, for example B .
$1 = - 2 \cdot 6 + t$
Solve for t .
$t = 1 - (- 2) \cdot 6 = 1 + 12 = 13$
Put together the equation of the line.
$y = m x + t = - 2 x + 13$

Calculate the side lengths and the perimeter of the triangle $A B C$ .

For this task you need the following basic knowledge: distance from a point
The perimeter of the triangle is calculated from the lengths of the segments between the points. Use the well-known formula.
$d (P_{1}, P_{2}) = \sqrt{(Δ x)^{2} + (Δ y)^{2}}$
Enter two points for each route.
Side AB:
$Δ x = - 2 - 6 = - 8$
$Δ y = 1 - 1 = 0$
Plug into the formula. Note that only positive results are relevant for lengths.
$d (A, B) = \sqrt{(- 8)^{2} + 0^{2}} = \sqrt{64} = 8$
So this side has length 8.
Side AC:
$Δ x = - 2 - 4 = - 6$
$Δ y = 1 - 5 = - 4$
Plug into the formula. Note that only positive results are relevant for lengths.
$d (A, C) = \sqrt{(- 6)^{2} + (- 4)^{2}} = \sqrt{36 + 16}$ $= \sqrt{52} \approx 7 a 21$
So this side is about length 7.2.
Side BC:
$Δ x = 6 - 4 = 2$
$Δ y = 1 - 5 = - 4$
Plug into the formula. Note that only positive results are relevant for lengths.
$d (A, C) = \sqrt{2^{2} + (- 4)^{2}} = \sqrt{4 + 16} = \sqrt{20} \approx 4 a 47$
So this side is about length 4.5.
$\Rightarrow$ The perimeter is equal to 8 + 7.2 + 4.5 = 19.7.

Calculate the area of the triangle $A B C$ .

$A = \frac{1}{2} \cdot Hight \cdot b a s e$
Choose AB as the base because it is parallel to the x-axis. This makes the height parallel to the y-axis.
Height h is equal to the distance from C to AB.
Since the height is parallel to the y-axis, the distance is calculated simply by comparing the y-coordinates.
The distance of point C from the baseline is $h = 5 - 1 = 4$
Inserted into the formula, this gives: $A = \frac{1}{2} \cdot 4 \cdot 8 = 16$

$3 x - 2$	$=$	$0$	$+ 2$
$3 x$	$=$	$2$	$: 3$
$x_{N1}$	$=$	$\frac{2}{3}$
	↓	The first line has a zero at $x_{N} = \frac{2}{3}$ .

$y$	$=$	$- \frac{3}{4} x + 1$
	↓	Set y=0 to determine the zero
$- \frac{3}{4} x + 1$	$=$	$0$	$- 1$
$- \frac{3}{4} x$	$=$	$- 1$	$: (- \frac{3}{4})$
$x$	$=$	$\frac{1}{\frac{3}{4}}$
	↓	You divide by a fraction $\to$ multiply by the reciprocal value
$x_{N2}$	$=$	$\frac{4}{3}$
	↓	The first line has a zero at $x_{N} = \frac{4}{3}$ .

$3 x - 2$	$=$	$- \frac{3}{4} x + 1$	$+ \frac{3}{4} x + 2$
$3 x + \frac{3}{4} x$	$=$	$1 + 2$
$3.75 x$	$=$	$3$	$: 3.75$
$x$	$=$	$\frac{3}{3.75}$
$x_{s}$	$=$	$0.8$
	↓	Plug $x_{s}$ into one of both functions
$y$	$=$	$3 \cdot 0.8 - 2$
$y$	$=$	$2.4 - 2$
$y_{s}$	$=$	$0.4$

$f (x)$	$>$	$0$
	↓	Insert the function term.
$0.4 x + 1$	$>$	$0$	$- 1$
	↓	Sort by x-terms and numbers.
$0.4 x$	$>$	$- 1$	$: 0.4$
	↓	Solve for x (observe $0.4 > 0$ , the inequality sign remains).
$x$	$>$	$- \frac{1}{0.4} = - 2.5$

$f (x)$	$>$	$0$
	↓	Insert functional equation.
$- 1.5 (x - 2)$	$>$	$0$
	↓	remove the brackets.
$- 1.5 x + 3$	$>$	$0$	$- 3$
	↓	Sort by x-terms and numbers.
$- 1.5 x$	$>$	$- 3$	$: (- 1.5)$
	↓	Solve for x. Watch out $- 1.5 < 0$ , so rotate the inequality sign.
$x$	$<$	$2$

$f (x)$	$>$	$0$
	↓	Insert functional equation.
$\frac{x}{5} - \frac{7}{5}$	$>$	$0$	$+ \frac{7}{5}$
	↓	Sort by x-terms and numbers.
$\frac{x}{5}$	$>$	$\frac{7}{5}$	$\cdot 5$
	↓	Solve for x (5>0, so no change to the inequality sign)
$x$	$>$	$7$

$2 x - 3$	$=$	$- 0.5 x + 4$	$+ 0.5 x \| + 3$
$2.5 x$	$=$	$7$	$: 2.5$
$x$	$=$	$2.8$
$y$	$=$	$2 \cdot 2.8 - 3$
	↓	Note "dot before dash"
$y$	$=$	$5.6 - 3 = 2.6$

Exercises: Linear functions as lines in coordinate systems

Drawing the graph

Determining the zeros

Determining the interscetion

Area of the triangle

Determine the height

Calculate baseline

Calculate the area

Illustration:

Straight line AB:

Straight line AC:

Straight line BC:

m=1−56−4=−42=−2

Side AB:

Δx=−2−6=−8

Δy=1−1=0

Side AC:

Δx=−2−4=−6

Δy=1−5=−4

Side BC:

Δx=6−4=2

Δy=1−5=−4

d(A,C)=22+(−4)2=4+16=20≈4a47

$m = \frac{1 - 5}{6 - 4} = \frac{- 4}{2} = - 2$

$Δ x = - 2 - 6 = - 8$

$Δ y = 1 - 1 = 0$

$Δ x = - 2 - 4 = - 6$

$Δ y = 1 - 5 = - 4$

$Δ x = 6 - 4 = 2$

$Δ y = 1 - 5 = - 4$

$d (A, C) = \sqrt{2^{2} + (- 4)^{2}} = \sqrt{4 + 16} = \sqrt{20} \approx 4 a 47$