Exercises: Curve discussion on rational functions

Hier musst du eine Kurvendiskussion einer gebrochen-rationalen Funktion durchführen.

Definitionsbereich bestimmen

Bestimme zunächst den Definitionsbereich.

Die Nullstellen von $x$ sind also $0$ und $3$. Daher ist der Defintionbereich von $f$:

${𝔻}_f=ℝ\backslash \{0;3\}$ .

Nullstellen

Bestimme die Nullstellen der Funktion.

Es gibt nur eine Nullstelle bei $x=-1$.

Grenzwertbetrachtung

Betrachte den Grenzwert an den Rändern des Definitionsbereichs (Intervallgrenzen, Lücken, im Unendlichen).

$${\displaystyle \underset{x\to -\infty }{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to -\infty }{\lim }\frac{\stackrel{\to 2}{\overbrace{2+\frac{2}{x}}}}{\underset{\to -\infty }{\underbrace{x-3}}}=0}$$

$${\displaystyle \underset{x\to \infty }{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to \infty }{\lim }\frac{\stackrel{\to 2}{\overbrace{2+\frac{2}{x}}}}{\underset{\to \infty }{\underbrace{x-3}}}=0}$$

$${\displaystyle \underset{x\to 0^{+}}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to 0^{+}}{\lim }\frac{\stackrel{\to 2}{\overbrace{2x+2}}}{\underset{\to 0^{-}}{\underbrace{x^2-3x}}}=-\infty }$$

$${\displaystyle \underset{x\to 0^{-}}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to 0^{-}}{\lim }\frac{\stackrel{\to 2}{\overbrace{2x+2}}}{\underset{\to 0^{+}}{\underbrace{x^2-3x}}}=\infty }$$

$${\displaystyle \underset{x\to 3^{+}}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to 3^{+}}{\lim }\frac{\stackrel{\to 8}{\overbrace{2x+2}}}{\underset{\to 0^{+}}{\underbrace{x^2-3x}}}=\infty }$$

$${\displaystyle \underset{x\to 3^{-}}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to 3^{-}}{\lim }\frac{\stackrel{\to 8}{\overbrace{2x+2}}}{\underset{\to 0^{-}}{\underbrace{x^2-3x}}}=-\infty }$$

Diese Grenzwerte geben dir eine waagerechte Asymptote bei $y=0$ und senkrechte Asymptoten bei $x=0$ und $x=3$.

Extrempunkte

Bestimme jetzt die Extrempunkte. Leite dafür die Funktion mit der Quotientenregel ab und setze sie gleich null.

$${\displaystyle f(x)=\frac{2x+2}{x^2-3x}}$$

$${\displaystyle f^{\prime }(x)=\frac{2\cdot (x^2-3x)-(2x+2)(2x-3)}{(x^2-3x{)}^2}}$$

$${\displaystyle f^{\prime }(x)=0}$$

$\iff 2\cdot (x^2-3x)-(2x+2)(2x-3)=0$

$\iff 2x^2-6x-4x^2-4x+6x+6=0$

$\iff -2x^2-4x+6=0^{}$

$${\displaystyle x_{1;2}=\frac{4\pm \sqrt{(-4{)}^2-4\cdot (-2)\cdot (6)}}{2\cdot (-2)}=\frac{4\pm \sqrt{64}}{-4}}$$

$\Rightarrow x_1=\frac{12}{-4}=-3$

$\Rightarrow x_2=\frac{-4}{-4}=1^{}$

Setze die Ergebnisse in die Funktion ein, um die ganzen Koordinaten zu erhalten.

$${\displaystyle f(x_1)=\frac{2\cdot (-3)+2}{(-3{)}^2-3\cdot (-3)}=\frac{-4}{9+9}=-\frac{2}{9}\Rightarrow E_1(-3|-\frac{2}{9})}$$

$f(x_2)=\frac{2\cdot 1+2}{1^2-3\cdot 1}=\frac{4}{-2}=-2\Rightarrow E_2(1|-2)$

Skizze

Hier musst du eine Kurvendiskussion einer gebrochen-rationalen Funktion durchführen.

Bestimmung des Definitionsbereichs D

Bestimme den Definitionsbereich. Der vorgelegte Funktionsterm ist ein Quotient. Daher kann der Nenner $N\left(x\right)=5x-5$ nicht Null werden. Da aber $\Rightarrow D=(R)\setminus 1$

Bestimmung der Nullstellen

Um die Nullstellen zu bestimmen, musst du überlegen, wann der Zähler des Quotienten Null ist.

$Z\left(x\right)=x^2+2x+3$ den Wert Null annehmen. Also:

$x^2+2x+3=0$

Quadratische Gleichungen kann man mit Hilfe der quadratischen Ergänzung lösen:

$x^2+2x+3=0\iff x^2+2x=-3\iff x^2+2x+1=-3+1\iff (x+1{)}^2=-2$

Da Quadrate nie negativ sein können, hat $g(x)={\displaystyle \frac{x^2+2x+3}{5x-5}}$ keine Nullstellen. Und die Definitionslücke $x_p=1$ ist eine Polstelle mit Vorzeichenwechsel.

Da der Zähler nie negativ wird, entscheidet nur der Nenner

$N\left(x\right)=5x-5=5(x-1)$ über das Vorzeichen von $g\left(x\right)$.

Links von x=1 ist $g\left(x\right)<0$ und rechts von x=1 ist $g\left(x\right)>0$.

Also ${\lim }_{x\to 1_{-}}=-\infty$ und ${\lim }_{x\to 1_{+}}=\infty$

Bestimmung der Asymptote

Da der Zählergrad, nämlich 2, größer als der Nennergrad, nämlich 1, ist, liegt eine schiefe Asymptote vor. Die asymtote wird durch Polynomdivision errechnet. Damit diese Polynomdivision "einfacher" klammere ich den Faktor $\frac{1}{5}$ aus.

Somit $(x^2+2x+3):(x-1)=x+3+{\displaystyle \frac{6}{x-1}}$

$\begin{array}{l}\phantom{-}(x^2+2x+3):(x-1)=x+3\\ \underline{-(x^2-x)}\\ \phantom{-(x^2+2x}3x+3\\ \phantom{(x^2+2x}\underline{-(3x-3)}\\ \phantom{-(x^2+2x+}6\end{array}$

Somit gilt für die Asymtote $a(x)={\displaystyle \frac{1}{5}}(x+3)$ und man schreibt den Term für g(x) in der Form: $g(x)={\displaystyle \frac{1}{5}}(x+3+{\displaystyle \frac{6}{x-1}})$

Um die Schnittpunkte mit der Asymtote zu berechnen, setzt man g(x)=a(x).

${\displaystyle \frac{1}{5}}(x+3+{\displaystyle \frac{6}{x-1}})={\displaystyle \frac{1}{5}}(x+3)\iff 6=0$

Somit gibt es keinen Schnittpunkt mit der Asymptote.

Extrema

Zur Ermittlung der Extrema berechnet man die 1. Ableitung und sucht deren Nullstellen.

$g(x)={\displaystyle \frac{1}{5}}{\displaystyle \frac{x^2+2x+3}{x-1}}$

$\Rightarrow g^{\prime }(x)={\displaystyle \frac{1}{5}}{\displaystyle \frac{(2x+2)(x-1)-1(x^2+2x+3)}{(x-1{)}^2}}={\displaystyle \frac{1}{5}}{\displaystyle \frac{2x^2+2x-2x-2-x^2-2x-3}{(x-1{)}^2}}$

$g^{\prime }(x)={\displaystyle \frac{1}{5}}{\displaystyle \frac{x^2-2x-5}{(x-1{)}^2}}$

$g^{\prime }(x)=0\iff x^2-2x-5=0\iff x^2-2x=5$

$x^2-2x+1=5+1\iff (x-1{)}^2=6$

$\iff x-1=\sqrt{6}\vee x-1=-\sqrt{6}$

$x_1=1+\sqrt{6}\approx \mathrm{3,45}\vee x_2=1-\sqrt{6}\approx -\mathrm{1,45}$

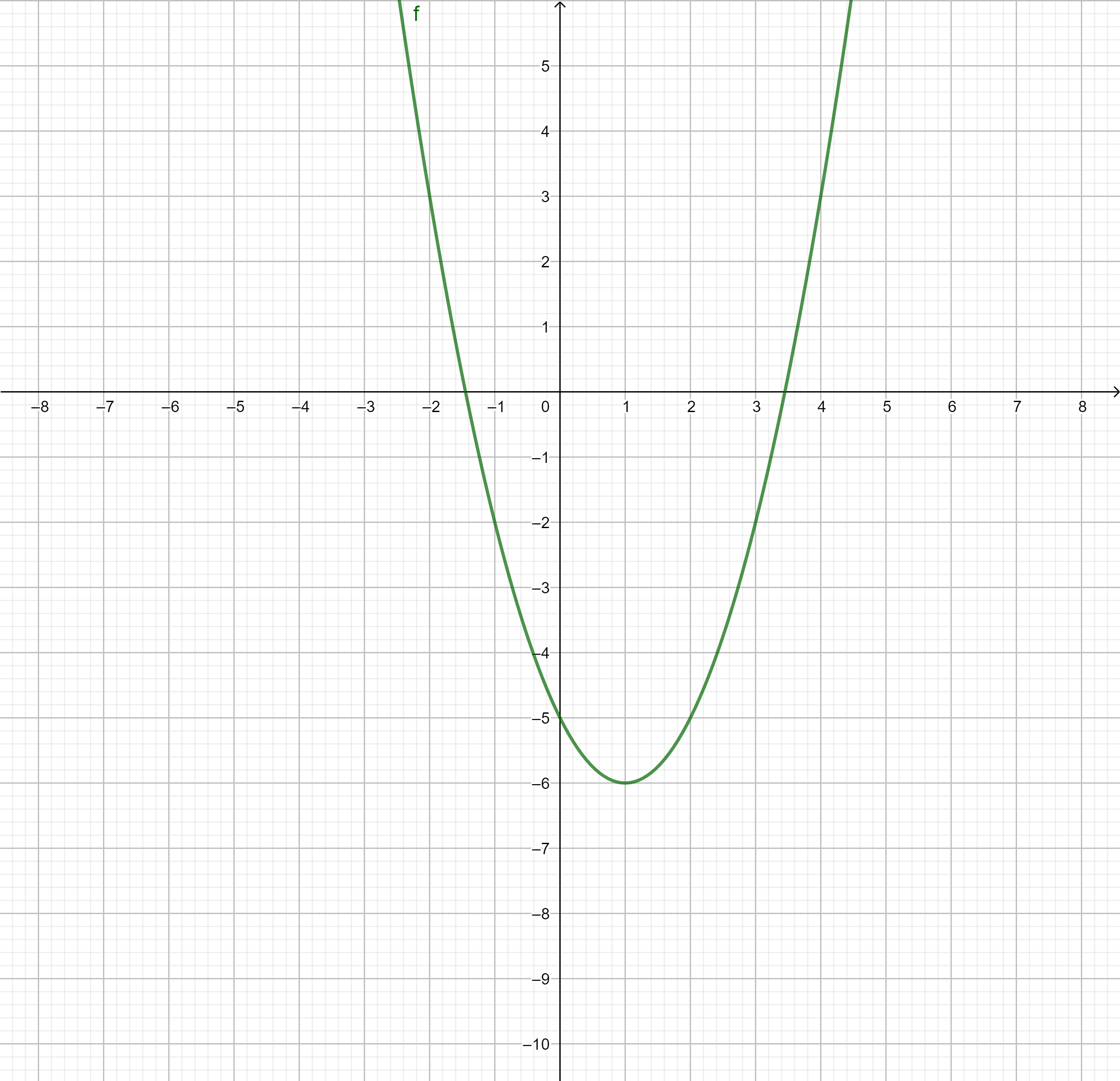
Graphisch ergibt sich für die vorzeichengleiche Funktion$z(x))=x^2-2x-5$ für $g^{\prime }(x)$ eine nach oben geöffnete Parabel mit den Nullstellen $x_1$ und$x_2$

Aus dem Graphen liest man ab: links von $x_1$ verläuft z oberhalb der x-Achse

und zwischen $x_1$ und $x_2$ verläuft z unterhalb der x- Achse

und rechts von $x_2$ verläuft z oberhalb der x-Achse

Somit gilt:

• $-\infty <x<1-\sqrt{6}\Rightarrow g^{\prime }(x)>0\Rightarrow g$ wächst

• $1-\sqrt{6}<x<1+\sqrt{6}\Rightarrow g^{\prime }(x)<0\Rightarrow g^{}$ fällt

• $1+\sqrt{6}<x<\infty \Rightarrow g^{\prime }(x)>0\Rightarrow g$ wächst

Also hat man ein Maximum bei $H\left(x_1\right)$und ein Minimum $T\left(x_2\right)$

In dieser Aufgabe geht es um die Kurvendiskussion einer gebrochen rationalen Funktion.

Die Lösung dieser Aufgabe findest du als Videolösung hier.

Definitionsbereich bestimmen

Wir bestimmen zunächst den Definitionsbereich: Der Funktionsterm $f(x)={\displaystyle \frac{x^2}{(x-\mathrm{0,5}{)}^3}}$ ist ein Bruch. Bei einem Bruch darf der Nenner

nicht null werden.

Ein Produkt ist genau dann gleich null, wenn wenigstens einer der Faktoren gleich null wird. Setze daher den Nenner der Funktion gleich 0, um die Definitionslücke zu bestimmen.

Nullstellenbestimmung

Die Nullstellen sind die Schnittpunkte des Funktionsgraphen mit der x-Achse.

$\Rightarrow NST=\left(0|0\right)$

Ableitungen bilden

1. Ableitung

$f(x)=\frac{x^2}{(x-\mathrm{0,5}{)}^3}$

Berechne die Ableitungen von Zähler ($u$) und Nenner ($v$). Für $v$ wird die Kettenregel verwendet.

$u^{\prime }=2x,v^{\prime }=3\cdot {(x-\mathrm{0,5})}^2$

Quotientenregel anwenden:

2. Ableitung

$f^{\prime }\left(x\right)=-\frac{x^2+x}{{(x-\mathrm{0,5})}^4}$

Berechne die Ableitungen von Zähler ($u$) und Nenner ($v$). Für $v$ wird die Kettenregel verwendet.

$u^{\prime }=2x+1,v^{\prime }=4\cdot {(x-\mathrm{0,5})}^3$

Quotientenregel anwenden:

Extrema bestimmen

Für die Extrema werden mithilfe der 1. Ableitung die x-Werte bestimmt:

$f^{\prime }\left(x\right)=-\frac{x^2+x}{{(x-\mathrm{0,5})}^4}$

Es wird nur der Zähler der ersten Ableitung gleich 0 gesetzt, da mit dem Nenner multipliziert werden kann und dieser dann wegfällt.

Art der Extrema bestimmen

$\Rightarrow$ Da $f^{\prime \prime }(-1)>0:$ Tiefpunkt

$\Rightarrow$ Da $f^{\prime \prime }\left(0\right)<0;$ Hochpunkt

y-Wert bestimmen

Die y-Koordinate des zweiten Extremums ist bereits bekannt, da dieses zusätzlich auch eine Nullstelle ist.

$\Rightarrow TP(-1|-\frac{8}{27}),HP\left(0|0\right)$