Calculate the distance of the line to the origin.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Slope/Gradient of a line
The shortest connection of any point on the line to the origin is a second line which passes through the origin and is perpendicular to .
Passing through the origin means .
Being perpendicular means
Plug in the known value of .
So the perpendicular line has the line equation .
Now calculate the intersection point of the two lines by setting equal their line equations.
↓ Plug in the line equations.
↓ Get the variable on the left side
Now substitute into one of the line equations to determine .
Plug in .
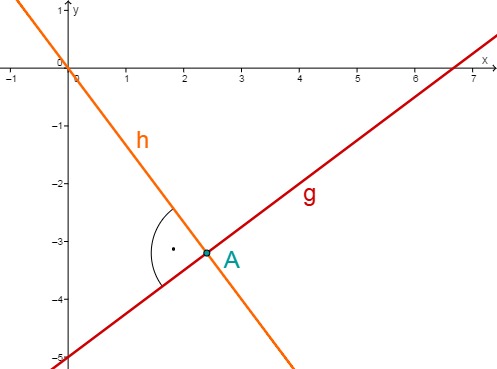
The intersection of the lines and is therefore at .
Now determine the distance of the origin to the calculated intersection point , this is exactly the shortest distance of the line to the origin.
Plug in the values.
Simplify.
The shortest distance of the line to the origin is therefore .
Do you have a question?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Slope/Gradient of a line
The shortest connection of any point on the line to the origin is a second line which passes through the origin and is perpendicular to .
Passing through the origin means .
Being perpendicular means
Plug in the known value of .
So the perpendicular line has the line equation .
Now calculate the intersection point of the two lines by setting equal their line equations.
↓ Plug in the line equations.
↓ Get the variable on the left side
↓ Get the 2 to the right side.
Now substitute into one of the line equations to determine .
Plug in .
The intersection of the lines and is therefore at .
Now determine the distance of the origin to the calculated intersection point , this is exactly the shortest distance of the line to the origin.
Plug in the values.
Simplify.
The shortest distance of the line to the origin is therefore approximately .

Do you have a question?
This content is licensed under
CC BY-SA 4.0 → Info
