The following function graphs are given:
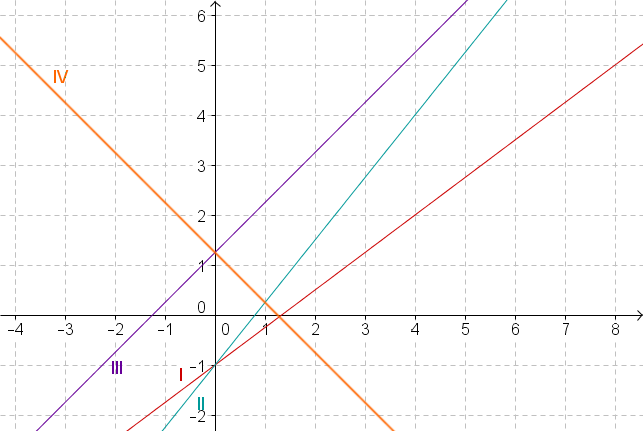
Which of the four graphs belongs to the equation y=45x−1 ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line Equations
You are given the graph equation: y=45x−1
You can read the slope and the y-intercept of this graph from the equation.
m=45
t=−1
First check for which functions the y-intercept is t=−1 by reading the y-value of each graph by cutting the y-axis.
Only graph I and II have the y-intercept −1 so you can exclude any other graph.
Now check which of the two graphs has the slope m=45 by going one unit to the right from the point x=0 and checking which of the two y-values increases by 45.
Both graphs start at the point P(0;−1). As the straight line you are looking for has a gradient of 45, it also passes through the point (0+4∣−1+5)=(4∣4).
Only line II runs through this point.
⇒ Graph II is the one that belongs to the given equation.
Do you have a question?
Wie lautet die Gleichung zum Graphen III?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line Equations
We have to check graph III
First read where the graph intersects the y-axis to determine the y-intercept.
The y-value of the point where the y-axis is intersected is y=1.25. Therefore, t=1.25.
Now read off how much the y-value changes if you go one to the right starting from x=0. This will give you the gradient.
The y-value increases from y=1.25 to y=2.25. The gradient is therefore m=12,25−1,25=11=1 .
Set up the equation.
⇒ Graph III has the equation y=x+1.25.
Do you have a question?
This content is licensed under
CC BY-SA 4.0 → Info
