Exercises: Finding line equations
The following diagrams contain graphs of linear functions. Determine the function terms.
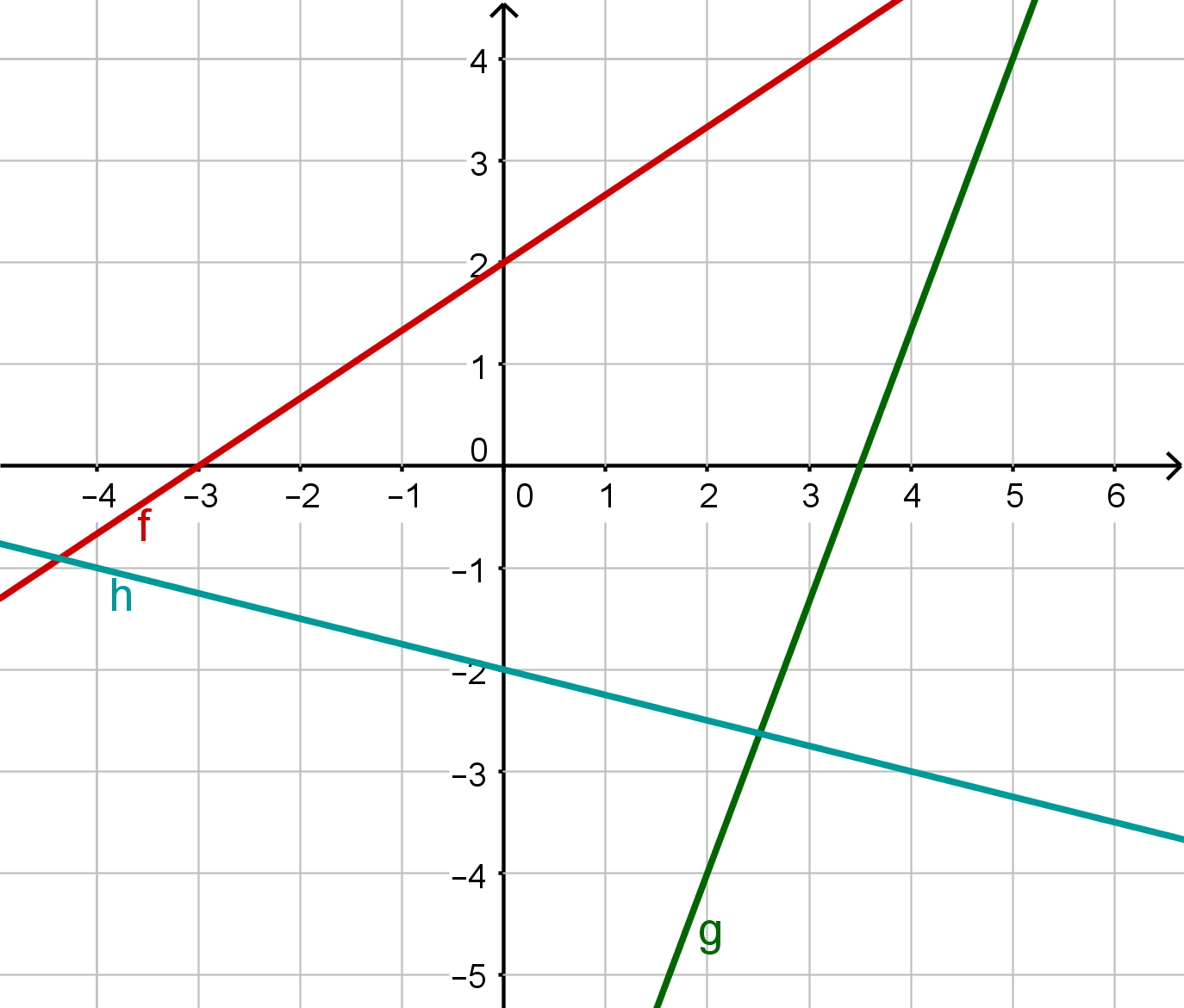
For this task you need the following basic knowledge: Linear Functions
Linear function
Set up the general form of a linear function.
Read off the y-intercept from the diagram.
Read off two points from the graph of the linear function to calculate the gradient:
You can use these points, for example:
and
and
For the gradient, you then get by substituting:
Now plug the calculated values of and into the general form:
Linear function
Set up the general form of a linear function.
Read off two points on the graph of the linear function to calculate the gradient.
For example, you can use these two points:
and
and
The gradient is then:
As the y-intercept is not visible, you have to calculate it. To do this, set up the equation of the line.
Insert one of the points, for example .
Now solve for .
Substitute the values of and into the general form of the linear function, and you will get the linear equation:
Linear function
Set up the general form of a linear function.
Read off two points from the graph of the linear function to calculate the gradient:
You can use these two points, for example:
and
and
Now use them to calculate the gradient:
Either read off or calculate the value. To calculate it, set up the linear equation.
Insert a point that lies on the straight line, for example .
Now, solve for .
Setze und in die allgemeine Form ein und du erhältst die Geradengleichung:
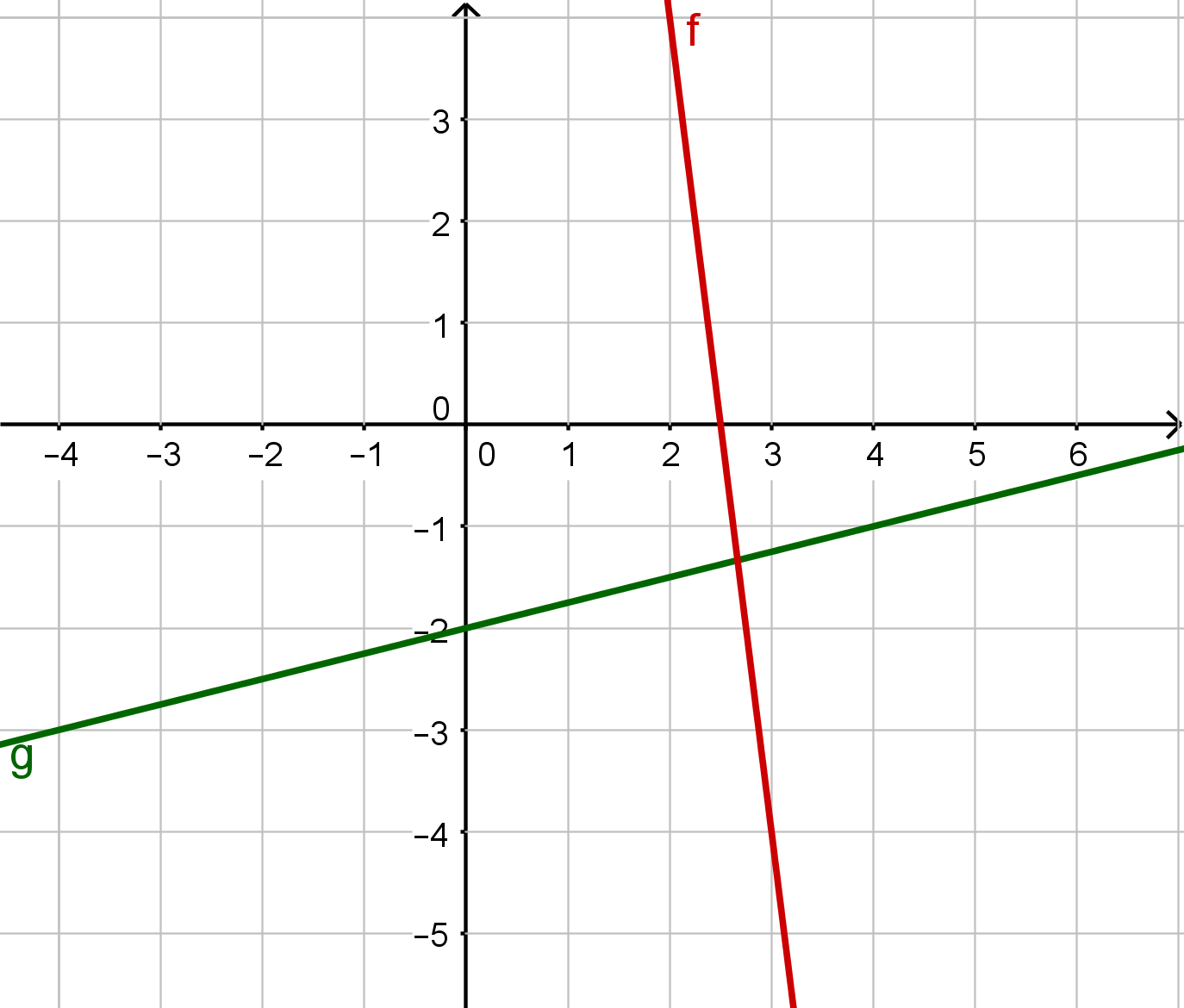
For this task you need the following basic knowledge: Linear Functions
Linear function
Set up the general form of a linear function.
Read off two points from the graph of the linear function to calculate the gradient:
You can use these two points, for example:
and
and
The result is a gradient:
As the y-intercept is not visible, you have to calculate it. Therefore, set up the equation of the line:
Insert one of the points, for example :
Solve for .
Plug and into the general form, and you will get the linear equation as a result:
Linear function
Set up the general form of a linear function.
Read off two points from the graph of the linear function to calculate the gradient:
You can use these two points, for example:
and
and
Now use them to calculate the gradient:
Read off the y-intercept from the diagram.
Plug and into the general form of the linear function, and you get the line equation of :