Set up the equation of the line through the two points and draw it.
P(2∣0) and Q(−2∣2)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line Equation
Determining the line equation
P(2∣0);Q(−2∣2)
Determine the gradient m of the general line equation y=m⋅x+t using the difference quotient.
m=−2−22−0=−42=−21
Plug m and the coordinates of a point, e.g. P(2∣0) into the general line equation and solve for t.
0=−21⋅2+t +21⋅2
t=1
Substitute m and t into the general line equation.
⇒ y=−21x+1
Drawing the line
Draw the two points P(2∣0) und Q(−2∣2) into the coordinate system and connect them to form a line.
Do you have a question?
P(0.5∣1.5) and Q(5∣3)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line Equation
Determining the line equation
P(0.5∣1.5);Q(5∣3)
Determine the gradient m of the general line equation y=m⋅x+t using the difference quotient.
m=5−0.53−1.5=4.51.5=31
Plug m and the coordinates of a point, e.g. Q(5∣3) into the general line equation and solve for t.
3=31⋅5+t∣−31⋅5
t=34
Substitute m and t into the general line equation.
⇒ y=31x+34
Drawing the line
Draw the two points P(0.5∣1.5) und Q(5∣3) into the coordinate system and connect them to form a line.
Do you have a question?
P(−2∣1) and Q(6∣4)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line Equation
Determining the line equation
P(−2∣1); Q(6∣4)
Determine the gradient m of the general line equation y=m⋅x+t using the difference quotient.
m=6−(−2)4−1=83
Plug m and the coordinates of a point, e.g. P(−2∣1) into the general line equation and solve for t.
1=83⋅(−2)+t
1=−86+t
1=−43+t∣+43
t=47
Substitute m and t into the general line equation.
⇒ y=83x+47
Drawing the line
Draw the two points P(−2∣1) und Q(6∣4) into the coordinate system and connect them to form a line.
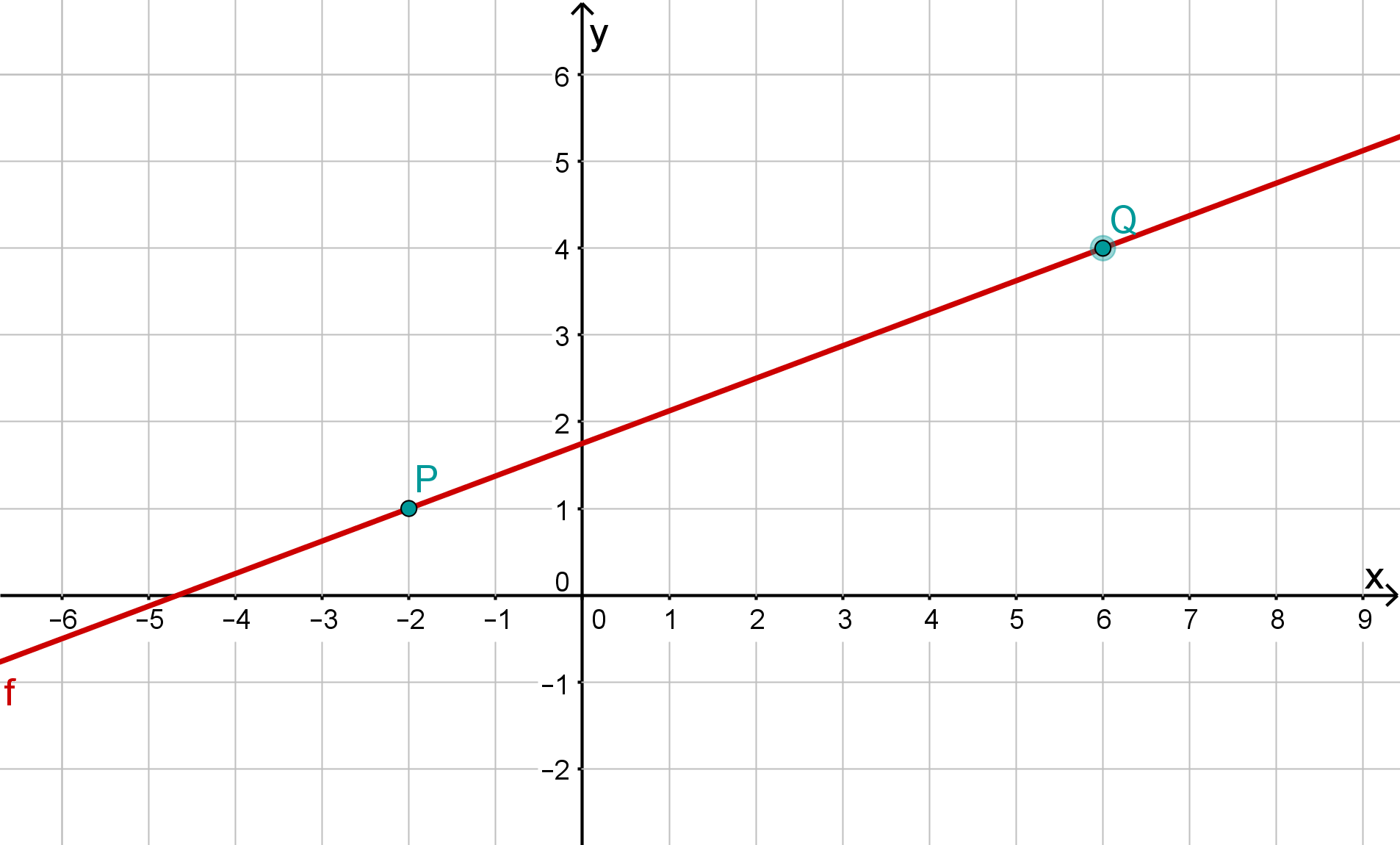
Do you have a question?
P(−4∣1) and Q(1∣−1)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line Equation
Determining the line equation
P(−4∣1); Q(1∣−1)
Determine the gradient m of the general line equation y=m⋅x+t using the difference quotient.
m=1−(−4)−1−1=−52
Plug m and the coordinates of a point, e.g. P(−4∣1) into the general line equation and solve for t.
1=−52⋅(−4)+t
1=58+t∣−58
t=−53
Substitute m and t into the general line equation.
⇒ y=−52x−53
Drawing the line
Draw the two points P(−4∣1) and Q(1∣−1) into the coordinate system and connect them to form a line.
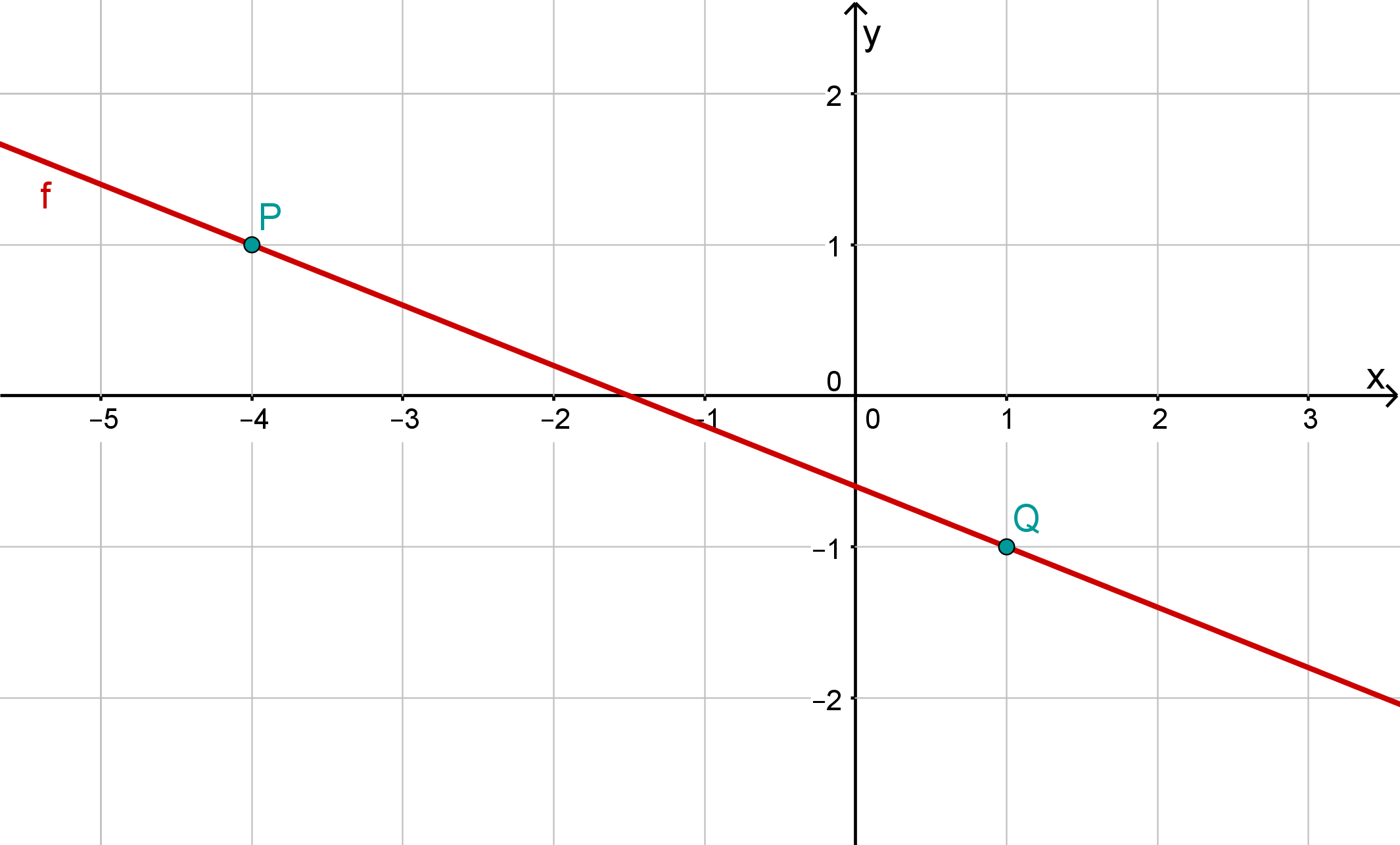
Do you have a question?
This content is licensed under
CC BY-SA 4.0 → Info


