A system of linear equations consists of several linear equations with common unknown variables. By Linear , we mean that each variable appears at most with the exponent 1.
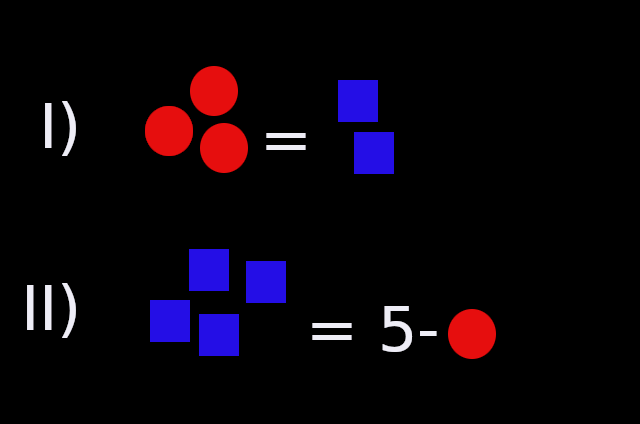
To solve a linear system of equations uniquely, you need at least as many equations as variables.
Example
As we have two variables (e.g. and or and ), we also need at least two equations to get uniqueness of the solution.
The equations are enumerated with Roman numerals and the variables are arranged appropriately one below the other. In the above example, all terms with are arranged one below the other, as well as all terms with .
Detailed introduction
You may find a step-by-step introduction in the course Introduction: Systems of Linear Equations - Part 1
Determination of systems of equations
More variables than equations
If a system of equations has more equations thanvariables, it usually cannot be solved uniquely. In the example, there are three unknowns but only two equations. In this case, we speak of an underdetermined system of equations.
It can also happen that such a system of equations has no solution. This case is explained in more detail in Solvability of linear systems.
Example:
Equal number of variables and equations
For a system of equations which has as many variables as equations, in most cases exactly one solution exists, i.e. the system of equations can be solved uniquely. This is what we consider as the normal case.
There are two exceptions:
If two or more equations are linearly dependent on each other, then the system of equations is again also not uniquely solvable, i.e. has an infinite number of solution combinations.
It can also happen that the system of equations has no solution. This is described in more detail under Solvability of linear systems.
Example:
More equations than variables
If a system of equations has more equations than variables for, there is, in most cases, no solution. In such a case, we speak of an overdetermined equation system.
Again, as an exception, if several equations are linearly dependent on each other. This can lead to the system becoming either uniquely solvable or we even have an underdetermined equation system.
Example:
Solving systems of equations
Solving a system of equations means determining all the variables so that all the equations of the system are satisfied. we will present five different methods to solve a system of equations:
The addition method
(if the addition of the equations cancels one of the unknown variables)
(if it is very easy to solve for a variable)
(when two equations can be easily solved for the same variable)
(when there are a lot of different variables)
(when a small system of equations is involved)
Writing a linear system as a matrix
A linear system of equations can always be written by an extended coefficient matrix .
Example:
The coefficients are transferred into the matrix. The constant terms are entered on the right and separated by a dash, in order to not confuse them with coefficients of variables.
The notation of a system of equations as an extended coefficient matrix is helpful to make statements about the Solvability of the linear system and to calculate the solution(s).
