Exercises: Sine, Cosine and Tangent on the unit circle
- 1
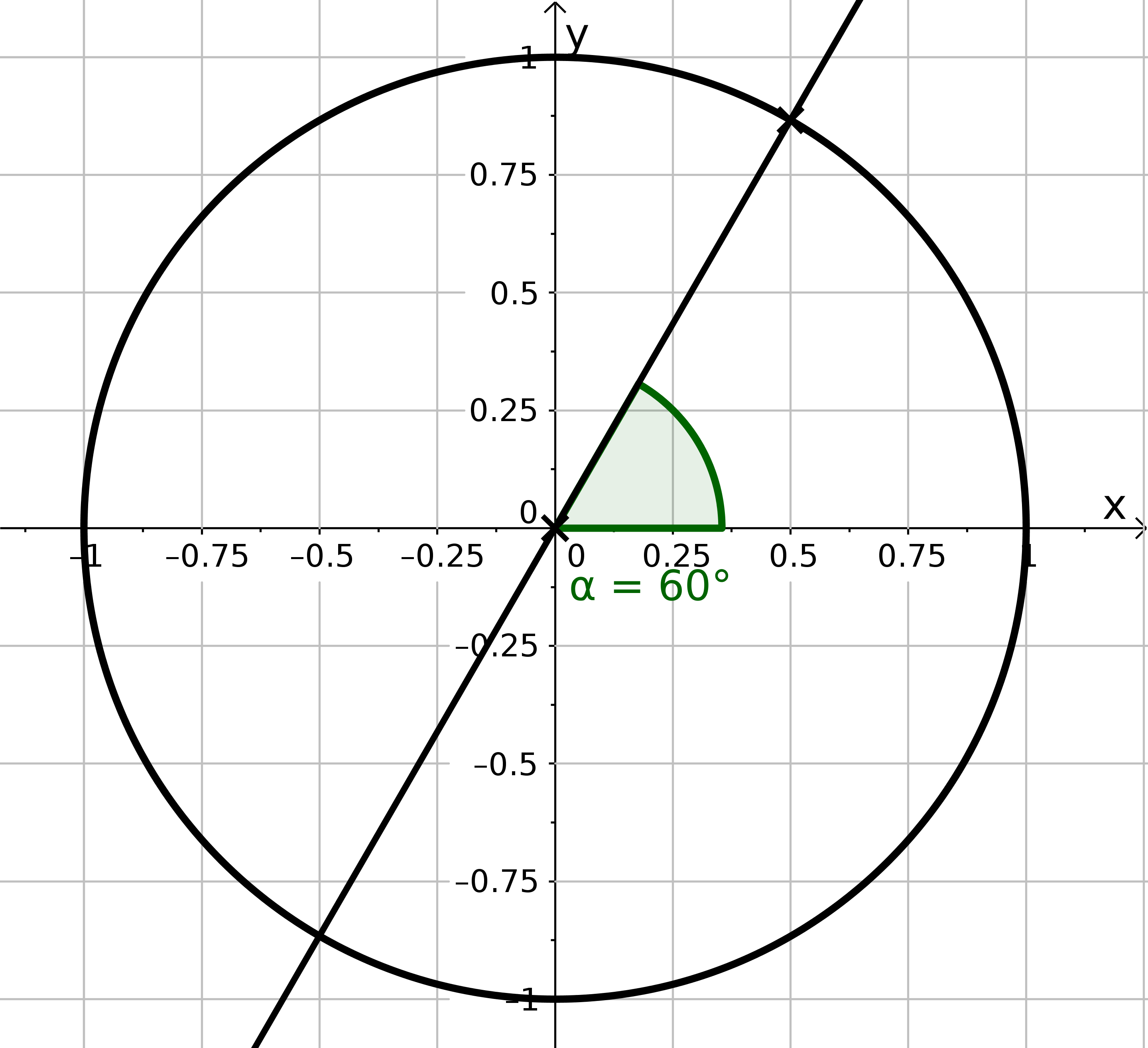
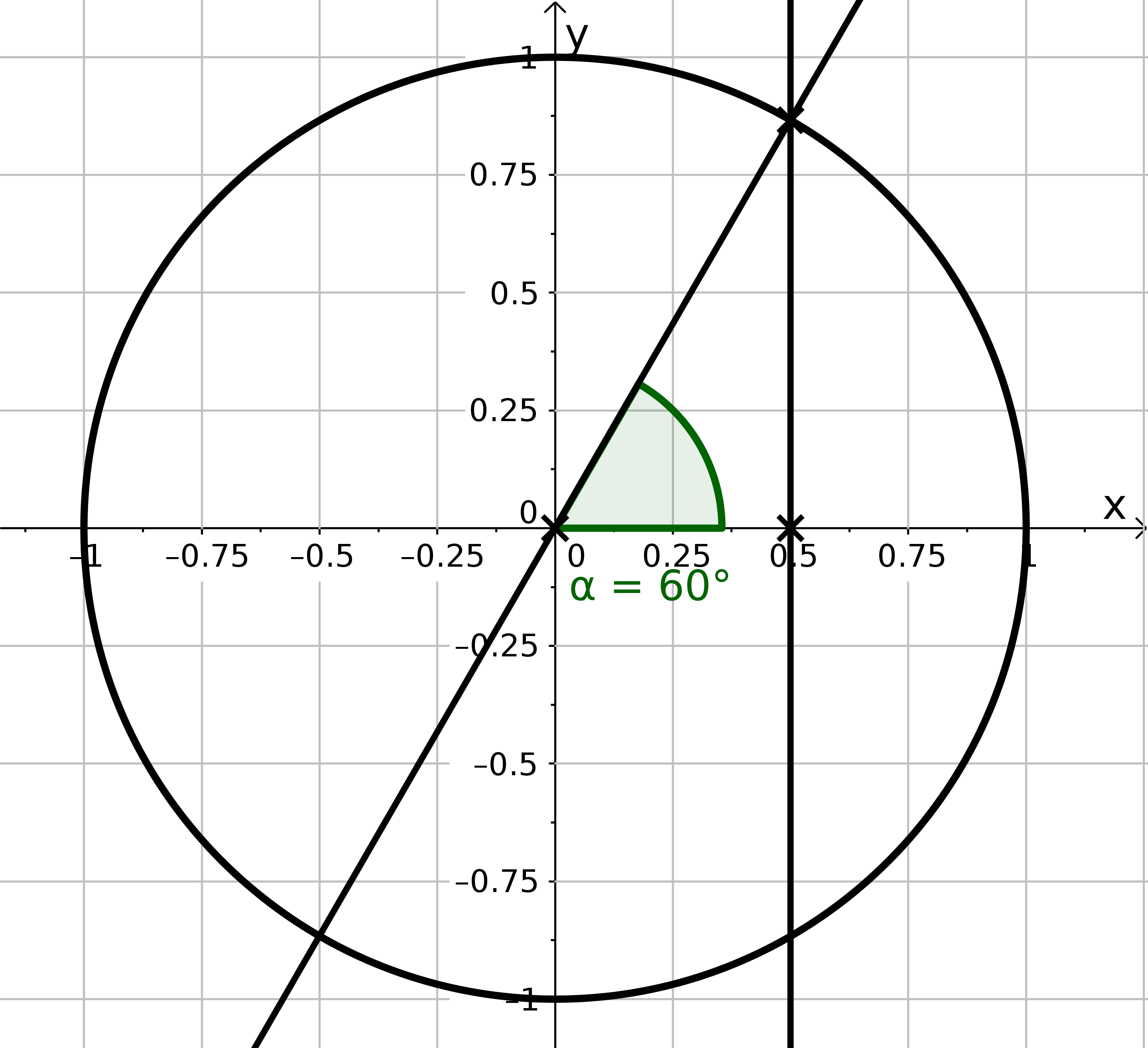
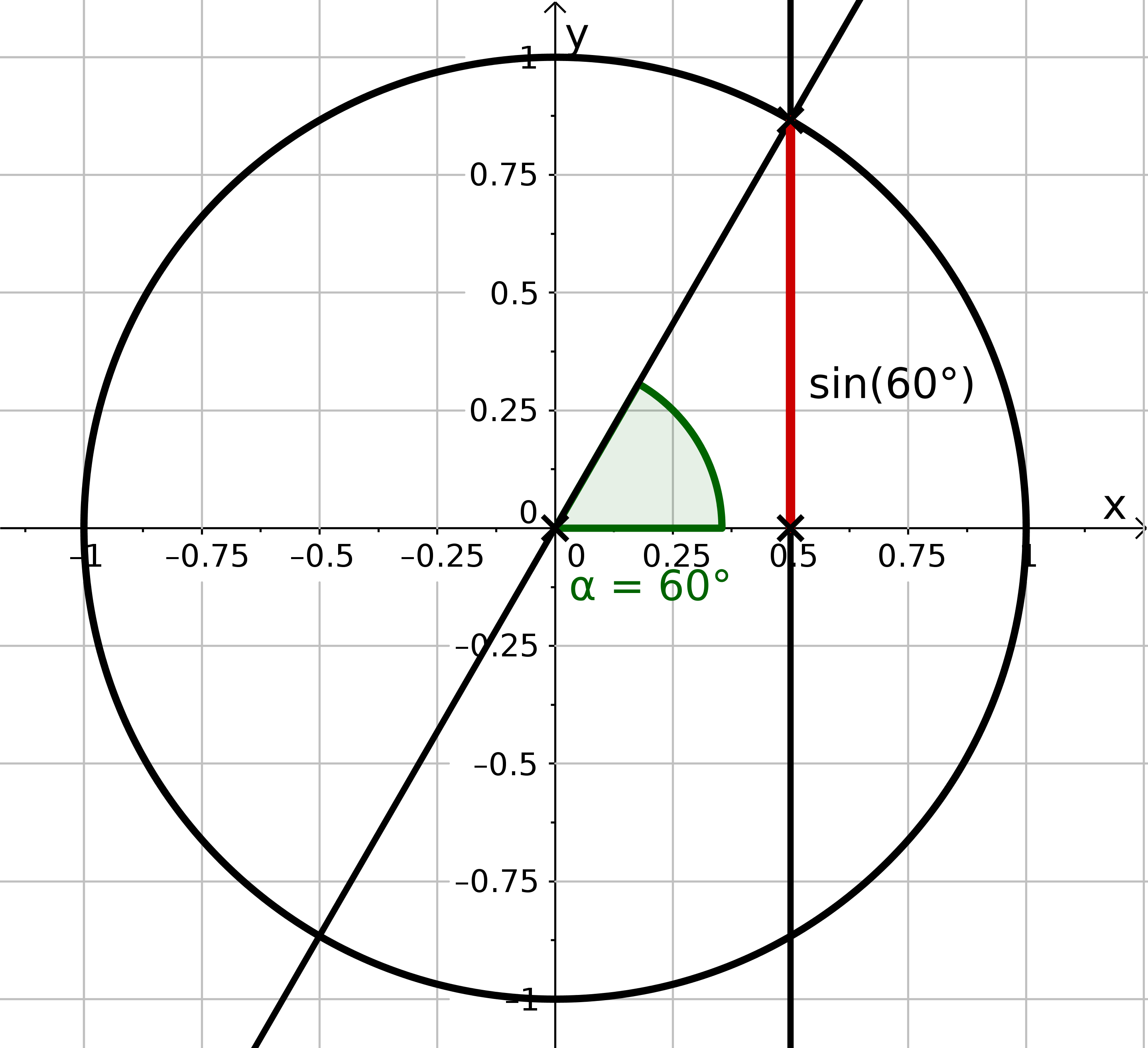
Consider on the unit circle: For which angles between and you have ?
- 2
Determine all solutions of the following equations in the range ( part (a) ) or (part (b) - (c) )
- 3
For which angles with do we have
- 4
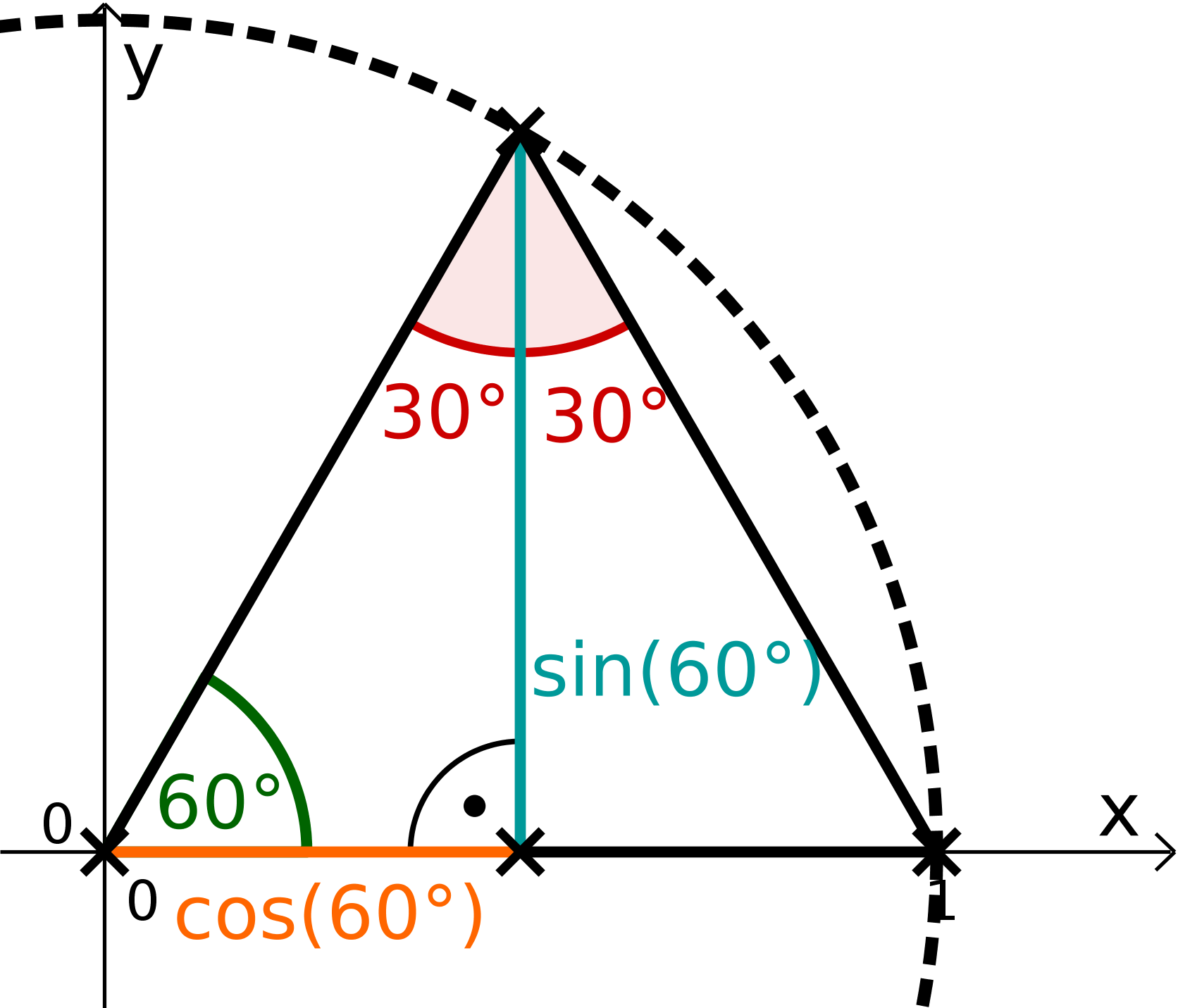
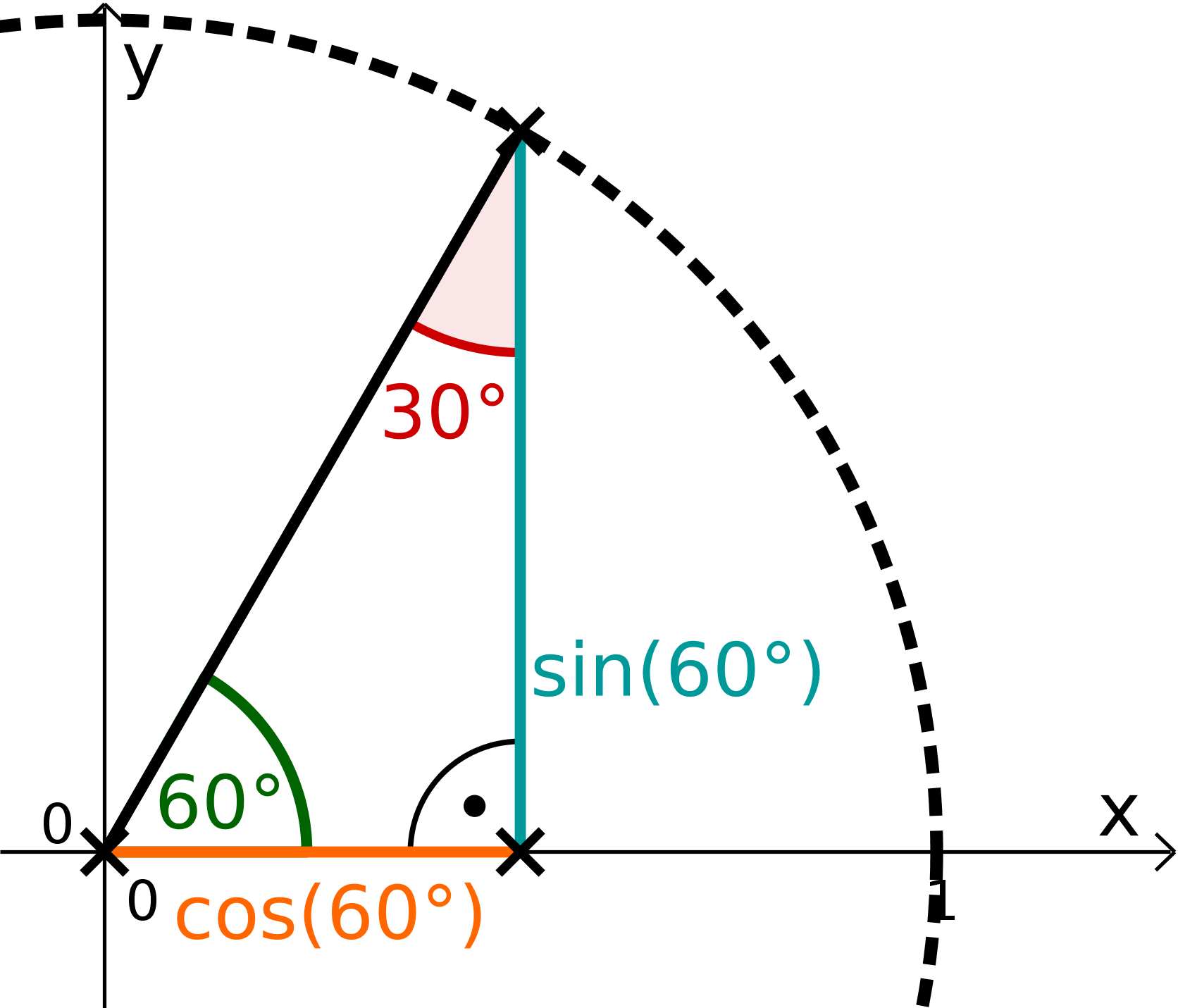
This exercise is about calculating , without knowing it before.
Draw a large coordinate system. (1 ). Construct the unit circle with the compass and apply a angle to the -axis with the set square. Construct the length and measure it with the ruler.
Calculate exactly. First find the value for . Construct an equilateral triangle for it.