Exercises: Distances, parallel and perpendicular lines

1
Determine the equation of the line that passes through the point $P$ and is perpendicular to the given line $y = m x + t$ .
$y = 3 x + 2$
$P (3 | 5)$

For this task you need the following basic knowledge: Slope/Gradient of a line
First determine the slope of the line $h$ perpendicular to $g (x) : y = 3 x + 2$ , where being perpendicular implies
$m_{2} = - \frac{1}{m_{1}}$
Plug in the known values.
$m_{2} = - \frac{1}{3}$
So the line we are looking for has a slope of $- \frac{1}{3}$ .
Now determine the $y$ -axis intercept of the line $h$ through $P (3 | 5)$ by substituting the point $P$ into the general line equation.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Plug in the values.
$5 = - \frac{1}{3} \cdot 3 + b | + 1$
Simplify and add $1$ .
$6 = b \Leftrightarrow b = 6$
So the line equation is $h (x) : y = - \frac{1}{3} x + 6$ .

$y = 0.5 x + 1$
$P (1 | 2)$

For this task you need the following basic knowledge: Slope/Gradient of a line
First determine the slope of the line $h$ perpendicular to $g (x) : y = 0.5 x + 1$ , where being perpendicular implies
$m_{2} = - \frac{1}{m_{1}}$
Plug in the known values.
$m_{2} = - \frac{1}{0.5} = - \frac{1}{\frac{1}{2}} = - 2$
So the line we are looking for has a slope of $- 2$ .
Now determine the $y$ -axis intercept of the line $h$ through $P (1 | 2)$ by substituting the point $P$ into the general line equation.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Plug in the values.
$2 = - 2 \cdot 1 + b$ $| + 2$
Simplify and add 2.
$4 = b \Rightarrow b = 4$
So the line equation is $h (x) : y = - 2 x + 4$ .

$y = - 5 x + 6$
$P (- 10 | 1)$

For this task you need the following basic knowledge: Slope/Gradient of a line
First determine the slope of the line $h$ perpendicular to $g (x) : y = - 5 x + 6$ , where being perpendicular implies
$m_{2} = - \frac{1}{m_{1}}$
Plug in the known values.
$m_{2} = - \frac{1}{- 5} = 0.2$
So the line we are looking for has a slope of $0.2$ .
Now determine the $y$ -axis intercept of the line $h$ through $P (- 10 | 1)$ by substituting the point $P$ into the general line equation.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Plug in the values.
$1 = 0.2 \cdot (- 10) + b$ $| + 2$
Simplify and add 2.
$3 = b \Rightarrow b = 3$
So the line equation is $h (x) : y = 0.2 x + 3$ .

$y = 4 x + 3$
$P (2 | - 5)$

For this task you need the following basic knowledge: Slope/Gradient of a line
First determine the slope of the line $h$ perpendicular to $g (x) : y = 4 x + 3$ , where being perpendicular implies
$m_{2} = - \frac{1}{m_{1}}$
Plug in the known values.
$m_{2} = - \frac{1}{4} = - 0.25$
So the line we are looking for has a slope of $- 0.25$ .
Now determine the $y$ -axis intercept of the line $h$ through $P (2 | - 5)$ by substituting the point $P$ into the general line equation.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Plug in the values.
$- 5 = - 0.25 \cdot 2 + b$ $+ 0.5$
Simplify and add $0.5$ .
$- 4.5 = b \Rightarrow b = - 4.5$
So the line equation is $h (x) : y = - 0.25 x - 4.5$ .

$y = - \frac{2}{3} x + 2$
$P (4 | 6)$

For this task you need the following basic knowledge: Slope/Gradient of a line
First determine the slope of the line $h$ perpendicular to $g (x) : y = - \frac{2}{3} x + 3$ , where being perpendicular implies
$m_{2} = - \frac{1}{m_{1}}$
Plug in the known values.
$m_{2} = - \frac{1}{- \frac{2}{3}} = \frac{3}{2}$
So the line we are looking for has a slope of $\frac{3}{2}$ .
Now determine the $y$ -axis intercept of the line $h$ through $P (4 | 6)$ by substituting the point $P$ into the general line equation.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Plug in the values.
$6 = \frac{3}{2} \cdot 4 + b$ $| - 6$
Simplify and subtract 6.
$0 = b \Rightarrow b = 0$
So the line equation is $h (x) : y = \frac{3}{2} x$ .

$y = \frac{1}{3} x - 2$
$P (2 | 5)$

For this task you need the following basic knowledge: Slope/Gradient of a line
First determine the slope of the line $h$ perpendicular to $g (x) : y = \frac{1}{3} x - 2$ , where being perpendicular implies
$m_{2} = - \frac{1}{m_{1}}$
Plug in the known values.
$m_{2} = - \frac{1}{\frac{1}{3}} = - 3$
So the line we are looking for has a slope of $- 3$ .
Now determine the $y$ -axis intercept of the line $h$ through $P (2 | 5)$ by substituting the point $P$ into the general line equation.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Plug in the values.
$5 = - 3 \cdot 2 + b$ $| + 6$
Simplify and add 6.
$11 = b \Rightarrow b = 11$
So the line equation is $h (x) : y = - 3 x + 11$ .
2
Determine the equation of the line $g$ that is parallel to the line $h$ and passes through the point $P$ .
$h$ : $y = 3 x - 2$ ; $P (1 | 0) $

For this task you need the following basic knowledge: Slope/Gradient of a line
$y = 3 x - 2$ ; $P (1 | 0)$
For the line to be parallel to $h$ , it must have the same slope.
The slope of a line is the variable $m$ of the general line equation.
$m = 3$
Setting up the line equation
Plug $m = 3$ and $P (1 | 0)$ into the the general line equation.
$0$ $=$ $3 \cdot 1 + t$ $- 3$
↓
solve for $t$
$t$ $=$ $- 3$
Plug $m$ and $t$ into the general line equation.
$\Rightarrow$ Line equation: $y = 3 x - 3$

$h$ : $y = x - 4$ ; $P (1 | 2) $

For this task you need the following basic knowledge: Slope/Gradient of a line
$y = x - 4$ ; $P (1 | 2)$
For the line to be parallel to $h$ , it must have the same slope.
The slope of a line is the variable $m$ of the general line equation.
$m = 1$
Setting up the line equation
Plug $m = 1$ and $P (1 | 2)$ into the the general line equation.
$2$ $=$ $1 + t$ $- 1$
↓
solve for $t$
$t$ $=$ $1$
Plug $m$ and $t$ into the general line equation.
$\Rightarrow$ Line equation: $y = x + 1$

$h$ : $y = 4 x$ ; $P (5 | 18) $

For this task you need the following basic knowledge: Slope/Gradient of a line
$y = 4 x$ ; $P (5 | 18)$
For the line to be parallel to $h$ , it must have the same slope.
The slope of a line is the variable $m$ of the general line equation.
$m = 4$
Setting up the line equation
Plug $m = 4$ and $P (5 | 18)$ into the the general line equation.
$18$ $=$ $4 \cdot 5 + t$ $- 20$
↓
solve for $t$
$t$ $=$ $- 2$
Plug $m$ and $t$ into the general line equation.
$\Rightarrow$ Line equation: $y = 4 x - 2$

$h$ : $y = - 2 x + 1$ ; $P (- 1 | 4)$

For this task you need the following basic knowledge: Slope/Gradient of a line
$y = - 2 x + 1$ ; $P (- 1 | 4)$
For the line to be parallel to $h$ , it must have the same slope.
The slope of a line is the variable $m$ of the general line equation.
$m = - 2$
Setting up the line equation
Plug $m = - 2$ and $P (- 1 | 4)$ into the the general line equation.
$4$ $=$ $- 2 \cdot (- 1) + t$ $- 2$
↓
solve for $t$
$t$ $=$ $2$
Plug $m$ and $t$ into the general line equation.
$\Rightarrow$ Line equation: $y = - 2 x + 2$
3
Determine the equation of the straight line through ...
the point $P (- 3 | 4)$ and being parallel to the $x$ -axis.

For this task you need the following basic knowledge: Line equation
Parallel to the $x$ -axis, means that the slope is $m = 0$ .
Plug $m$ and $P$ into the general line equation.
$\begin{array}{rcl} 4 & = & 0 \cdot (- 3) + t \\ 4 & = & t \end{array}$
Assemble to a line equation.
$y = 0 \cdot x + 4 = 4$

the point $Q (2 | 5)$ and is parallel to the bisector of the 2nd quadrant (the diagonal pointing down).

For this task you need the following basic knowledge: Line equation
Parallel to the bisector of the 2nd quadrant means the line has the same slope as the bisector.
The slope of the bisector of the 2nd quadrant is -1
$\Rightarrow m = - 1$
Plug $m$ into the straight line equation in order to calculate $t$ .
$\begin{array}{rcl} 5 & = & - 2 + t & | + 2 \\ t & = & 7 \end{array}$
Plug $m$ and $t$ into the general equation of a straight line.
$y = - 1 \cdot x + 7 = - x + 7$

the point $R (- 4 | 2)$ and is parallel to the $y$ -axis.

For this task you need the following basic knowledge: Line equation
Parallel to the $y$ -axis means that there is no function equation, since an $x$ -value is assigned an infinite number of $y$ -values.
The straight line can therefore only be described as the $x$ -value of $R$ .
$\Rightarrow x = - 4$

the point $S (2 | - 3)$ and is parallel to the bisector of the 1st quadrant (the diagonal pointing up).

For this task you need the following basic knowledge: Line equation
The line being parallel to the bisector of the 1st quadrant means it has the same slope.
The slope of the bisector of the 1st quadrant is $1$ .
$\Rightarrow m = 1$
Substitute $m$ and $S$ into the general line equation and solve for $t$ .
$\begin{array}{rcl} - 3 & = & 2 + t & | - 2 \\ t & = & - 5 \end{array}$
Substitute $m$ and $t$ into the general line equation.
$\Rightarrow y = x - 5$

the origin and is parallel to the straight line $AB$ with $A (- 72 | - 60)$ and $B (- 24 | - 20)$ .

For this task you need the following basic knowledge: Line equation
Passing through the origin means, the $y$ -axis intercept is $t = 0$ .
Being parallel to the straight line $AB$ means that the line has the same slope as $AB$ .
$A (- 72 | - 60); B (- 24 | - 20)$
Calculate the slope $m$ using the difference quotient .
$m = \frac{- 20 - (- 60)}{- 24 - (- 72)} = \frac{40}{48} = \frac{5}{6}$
Substitute $m$ and $t$ into the general line equation.
$\Rightarrow y = \frac{5}{6} x$
4
Two perpendicular lines intersect at $S (- 2 | - 1)$ .
Determine at least one possible line equations.

For this task you need the following basic knowledge: Linear function
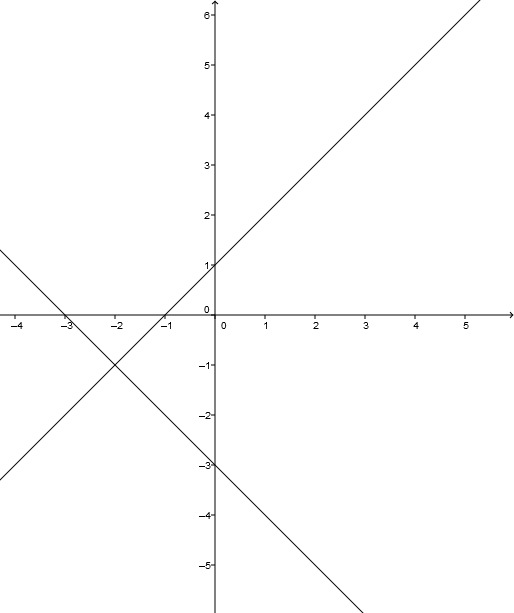
We need to construct two perpendicular lines with the point of intersection $(- 2, - 1)$ . As you can already see from the problem setting, there are several ways to choose two such straight lines. One possibility is given below. A good criterion to check whether the two chosen straight lines are perpendicular to each other is to check whether $m_{1} \cdot m_{2} = - 1$ .
For instance, choose the line $g$ with $y = g (x) = x + 1$ and $h$ with $y = h (x) = - x - 3$ . Then $m_{1} \cdot m_{2} = 1 \cdot (- 1) = - 1$ and we have $g (- 2) = - 1$ and $h (- 2) = - 1$ . So the point of intersection is on the two lines and they are perpendicular to each other.
Caution:
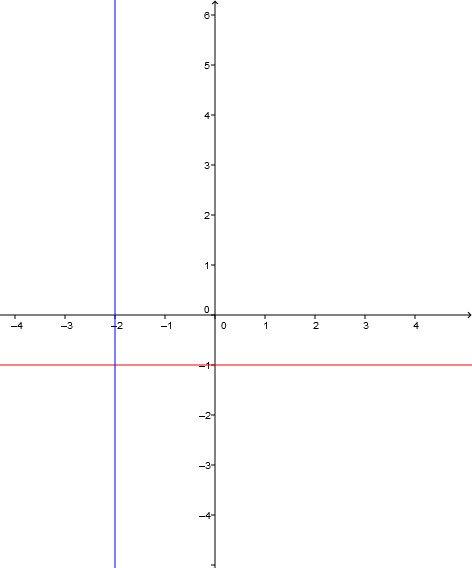
You may also choose the line $y = - 1$ , which is parallel to the $x$ -axis and passes through the point $(- 2, - 1)$ . Then there is exactly one line perpendicular to it and passing through this point, namely that one given by $x = - 2$ and running parallel to the $y$ - axis. However, $x = - 2$ does not describe a function but a relation!
5
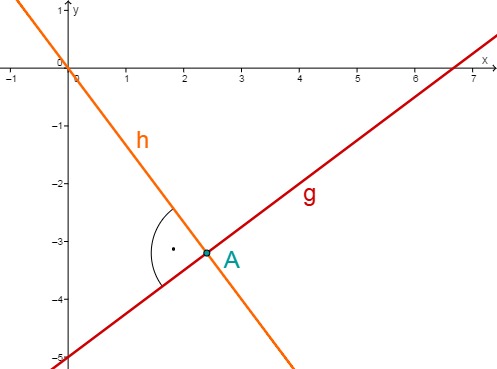
Calculate the distance of the line to the origin.
$y = \frac{3}{4} x - 5$

For this task you need the following basic knowledge: Slope/Gradient of a line
The shortest connection of any point on the line $g (x) : y = m_{1} \cdot x + b$ to the origin is a second line $h (x) : y = m_{2} \cdot x + b_{2}$ which passes through the origin and is perpendicular to $g$ .
Passing through the origin means $h (0) = b_{2} = 0$ .
Being perpendicular means
$m_{2} = - \frac{1}{m_{1}}$
Plug in the known value of $m_{1}$ .
$m_{2} = - \frac{1}{\frac{3}{4}} = - \frac{4}{3}$
So the perpendicular line has the line equation $h (x) : y = - \frac{4}{3} x$ .
Now calculate the intersection point $A (x_{s} | y_{s})$ of the two lines by setting equal their line equations.
$g (x_{s})$ $=$ $h (x_{s})$
↓
Plug in the line equations.
$- \frac{4}{3} x_{s}$ $=$ $\frac{3}{4} x_{s} - 5$ $- \frac{3}{4} x_{s}$
↓
Get the variable $x_{s}$ on the left side
$- \frac{25}{12} x_{s}$ $=$ $- 5$ $\cdot (- 1)$
$\frac{25}{12} x_{s}$ $=$ $5$ $: \frac{25}{12}$
$x_{s}$ $=$ $\frac{12}{5}$
$=$ $2.4$
Now substitute $x_{s}$ into one of the line equations to determine $y_{s}$ .
$h (x_{s}) : y_{s} = - \frac{4}{3} x_{s}$
Plug in $x_{s} = 2.4$ .
$y_{s} = - \frac{4}{3} \cdot 2.4 = - 3.2$
The intersection of the lines $h$ and $g$ is therefore at $A (2.4 | - 3.2)$ .
Now determine the distance of the origin to the calculated intersection point $A$ , this is exactly the shortest distance of the line $g$ to the origin.
$d = \sqrt{(x_{s} - x_{0})^{2} + (y_{s} - y_{0})^{2}}$
Plug in the values.
$d = \sqrt{(2.4 - 0)^{2} + (- 3.2 - 0)^{2}}$
Simplify.
$= \sqrt{5.76 + 10.24} = \sqrt{16} = 4$
The shortest distance of the line $g$ to the origin is therefore $4$ .

$y = - \frac{1}{2} x + 2$

For this task you need the following basic knowledge: Slope/Gradient of a line
The shortest connection of any point on the line $g (x) : y = m_{1} \cdot x + b$ to the origin is a second line $h (x) : y = m_{2} \cdot x + b_{2}$ which passes through the origin and is perpendicular to $g$ .
Passing through the origin means $h (0) = b_{2} = 0$ .
Being perpendicular means
$m_{2} = - \frac{1}{m_{1}}$
Plug in the known value of $m_{1}$ .
$m_{2} = - \frac{1}{- \frac{1}{2}} = 2$
So the perpendicular line has the line equation $h (x) : y = 2 x$ .
Now calculate the intersection point $A (x_{s} | y_{s})$ of the two lines by setting equal their line equations.
$g (x_{s})$ $=$ $h (x_{s})$
↓
Plug in the line equations.
$- \frac{1}{2} x_{s} + 2$ $=$ $2 x_{s}$ $- 2 x_{s}$
↓
Get the variable $x_{s}$ on the left side
$- 2.5 x_{s} + 2$ $=$ $0$ $- 2$
↓
Get the 2 to the right side.
$- 2.5 x_{s}$ $=$ $- 2$ $: (- 2.5)$
$x_{s}$ $=$ $0.8$
Now substitute $x_{s}$ into one of the line equations to determine $y_{s}$ .
$h (x_{s}) : y_{s} = 2 x_{s}$
Plug in $x_{s} = 0.8$ .
$y_{s} = 2 \cdot 0.8 = 1.6$
The intersection of the lines $h$ and $g$ is therefore at $A (0.8 | 1.6)$ .
Now determine the distance of the origin to the calculated intersection point $A$ , this is exactly the shortest distance of the line $g$ to the origin.
$d = \sqrt{(x_{s} - x_{0})^{2} + (y_{s} - y_{0})^{2}}$
Plug in the values.
$d = \sqrt{(0.8 - 0)^{2} + (1.6 - 0)^{2}}$
Simplify.
$= \sqrt{0.64 + 2.56} = \sqrt{3.2} \approx 1.79$
The shortest distance of the line $g$ to the origin is therefore approximately $1.79$ .
6
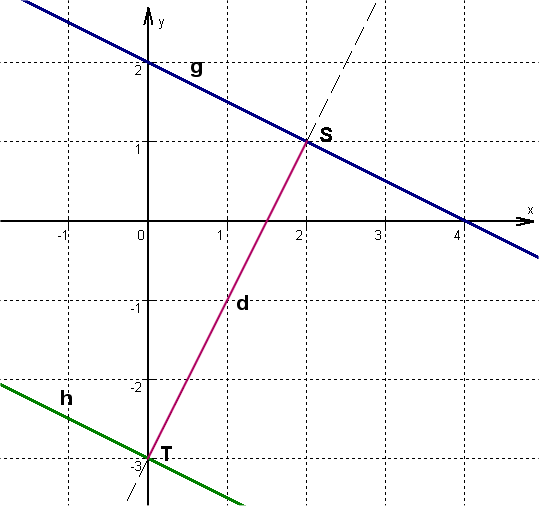
Calculate the distance of the parallel lines g: $y = - \frac{1}{2} x + 2$ and h: $y = - \frac{1}{2} x - 3$ .

Distance between two parallel lines
The shortest path between two parallel lines can be read off along a normal (=perpendicular line) of the two parallel lines .
The distance of the straight lines is equal to the distance between the two intersection points of the normal line with the parallel lines .
Sketch
The construction looks as follows:
Line equation
Establish the line equation of the normal line d.
First calculate the slope.
$m_{d} \cdot m_{g}$ $=$ $- 1$ $: m_{g}$
$m_{d}$ $=$ $\frac{- 1}{m_{g}}$
↓
Plug in the slope $m_{g} = - \frac{1}{2}$
$m_{d}$ $=$ $\frac{- 1}{- \frac{1}{2}}$
↓
Simplify the right-hand side
$m_{d}$ $=$ $- 2$
Now set up the line equation.
For this, you need a point $T$ , which lies on line h. For instance, you may take the $y$ -axis intercept of $h (x)$ , which is $T (0 | - 3)$ . But any other point is also correct.
Plug $T (0 | - 3)$ and $m_{d}$ into the general line equation for d to get the parameter $t$ .
$- 3$ $=$ $2 \cdot (0) + t$
↓
multiply out
$t$ $=$ $- 3$
↓
Plug $t$ and $m_{d}$ into the general line equation.
$y$ $=$ $2 x - 3$
Determine the intersection of d and g
First calculate the $x$ -coordinate of the intersection point $S$ .
Normal line d: $y = 2 x - 3$
Paralle line g: $y = - \frac{1}{2} x + 2$
Equate both function equations:
$2 x - 3$ $=$ $- \frac{1}{2} x + 2$ $+ 3$
$2 x$ $=$ $- \frac{1}{2} x + 5$ $+ \frac{1}{2} x$
$\frac{5}{2} x$ $=$ $5$ $: \frac{5}{2}$
$x$ $=$ $2$
Now calculate the $y$ -coordinate of the intersection point $S$ .
$y$ $=$ $2 x - 3$
↓
Plug in x = 2 .
$y$ $=$ $2 \cdot 2 - 3$
↓
compute
$y$ $=$ $1$
Hence the point $S$ has the following coordinates:
$\Rightarrow$ $S (2 | 1)$
Determine the distance between points S and T.
Determine the distance in $x$ -direction.
$T (0 | - 3)$ , $S (2 | 1)$
Calculate the difference of the $x$ -values of $S$ and $T$ .
$Δ x = 2 - 0 = 2$
Determine the distance in $y$ -direction.
$T (0 | - 3)$ , $S (2 | 1)$
Calculate the difference of the $y$ -values.
$Δ y = 1 - (- 3) = 4$
Determine the distance in a direct line between the points.
$Δ x = 2$
$Δ y = 4$
This is done by the Pythagoraen Theorem:
$d^{2}$ $=$ $2^{2} + 4^{2}$
↓
compute both squares
$d^{2}$ $=$ $4 + 16$
↓
add
$d^{2}$ $=$ $20$
↓
take the root
$d^{}$ $=$ $\sqrt{20}$
If you enter $\sqrt{20}$ into a calculator and round the result to two decimal places, you get:
$d = \sqrt{20} \approx 4.47$
Result
The distance between the two lines is $d = \sqrt{20} \approx 4.47$ .
7
Consider the equation $y = \frac{3}{2} x + 1$ .
Zeichne die Gerade zu der Gleichung in ein Koordinatensystem.

For this task you need the following basic knowledge: Lines in coordinate systems
Choose any point on the line, e.g. the $y$ -axis-intercept $(0 | 1)$ , and go two to the right and three upwards, which corresponds to a slope of $m = \frac{3}{2}$ . Connect the two points to obtain a straight line.

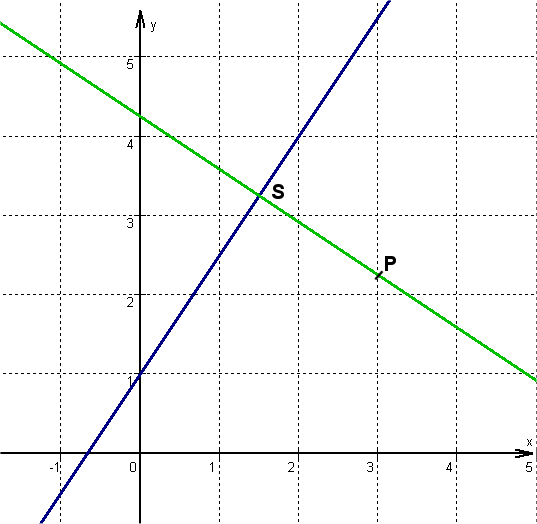
Set up the equation of the perpendicular line through the point $P (3 | 2.25)$ .

For this task you need the following basic knowledge: Slope/Gradient of a line
You obtain the slope of the perpendicular (=normal) line by dividing -1 by the original slope.
$m$ $=$ $- 1 : \frac{3}{2} = \frac{- 1}{1} \cdot \frac{2}{3} = - \frac{2}{3}$
↓
Plug the coordinates of $P$ and $m$ into the general line equation.
$2.25$ $=$ $- \frac{2}{3} \cdot 3 + t$
$=$ $- \frac{6}{3} + t$
$=$ $- \frac{2}{1} + t$
$=$ $- 2 + t$ $+ 2$
↓
Solve for $t$ .
$t$ $=$ $2.25 + 2 = 4.25$
Substitute $m$ and $t$ into the general line equation.
$y$ $=$ $- \frac{2}{3} x + 4.25$

Draw the line in the same coordinate system as the line from exercise 1.

For this task you need the following basic knowledge: Slope/Gradient of a line
Choose any point on the line, e.g. the given point $P (3 | 2.25)$ and go, according to the gradient $m = - \frac{2}{3}$ , $3$ units to the left and $2$ units upwards. Connect the two points to obtain a straight line. (see sketch in subtask 1)

Calculate the intersection of the two lines.

Calculating the $x$ -coordinate
Set the straight line functions equal to obtain the point of intersection.
$\frac{3}{2} x + 1$ $=$ $- \frac{2}{3} x + \frac{17}{4}$ $+ \frac{2}{3} x | - 1$
↓
Get $x$ to one side.
$\frac{3}{2} x + \frac{2}{3} x$ $=$ $\frac{17}{4} - 1$
↓
Factor out $x$ and add the fractions.
$\frac{13}{6} x$ $=$ $\frac{13}{4}$ $: \frac{13}{6}$
$x$ $=$ $\frac{6}{4} = \frac{3}{2} = 1.5$
Calculating the $y$ -coordinate

Plug $x$ into one of the line equations, e.g. that of the given line.
$y$ $=$ $\frac{3}{2} \cdot \frac{3}{2} + 1$
$=$ $\frac{9}{4} + 1$
$=$ $3.25$
$\Rightarrow$ S $(1.5 | 3.25)$

$g (x_{s})$	$=$	$h (x_{s})$
	↓	Plug in the line equations.
$- \frac{4}{3} x_{s}$	$=$	$\frac{3}{4} x_{s} - 5$	$- \frac{3}{4} x_{s}$
	↓	Get the variable $x_{s}$ on the left side
$- \frac{25}{12} x_{s}$	$=$	$- 5$	$\cdot (- 1)$
$\frac{25}{12} x_{s}$	$=$	$5$	$: \frac{25}{12}$
$x_{s}$	$=$	$\frac{12}{5}$
	$=$	$2.4$

$m_{d} \cdot m_{g}$	$=$	$- 1$	$: m_{g}$
$m_{d}$	$=$	$\frac{- 1}{m_{g}}$
	↓	Plug in the slope $m_{g} = - \frac{1}{2}$
$m_{d}$	$=$	$\frac{- 1}{- \frac{1}{2}}$
	↓	Simplify the right-hand side
$m_{d}$	$=$	$- 2$

$- 3$	$=$	$2 \cdot (0) + t$
	↓	multiply out
$t$	$=$	$- 3$
	↓	Plug $t$ and $m_{d}$ into the general line equation.
$y$	$=$	$2 x - 3$

$2 x - 3$	$=$	$- \frac{1}{2} x + 2$	$+ 3$
$2 x$	$=$	$- \frac{1}{2} x + 5$	$+ \frac{1}{2} x$
$\frac{5}{2} x$	$=$	$5$	$: \frac{5}{2}$
$x$	$=$	$2$

$y$	$=$	$2 x - 3$
	↓	Plug in x = 2 .
$y$	$=$	$2 \cdot 2 - 3$
	↓	compute
$y$	$=$	$1$

$d^{2}$	$=$	$2^{2} + 4^{2}$
	↓	compute both squares
$d^{2}$	$=$	$4 + 16$
	↓	add
$d^{2}$	$=$	$20$
	↓	take the root
$d^{}$	$=$	$\sqrt{20}$

$m$	$=$	$- 1 : \frac{3}{2} = \frac{- 1}{1} \cdot \frac{2}{3} = - \frac{2}{3}$
	↓	Plug the coordinates of $P$ and $m$ into the general line equation.
$2.25$	$=$	$- \frac{2}{3} \cdot 3 + t$
	$=$	$- \frac{6}{3} + t$
	$=$	$- \frac{2}{1} + t$
	$=$	$- 2 + t$	$+ 2$
	↓	Solve for $t$ .
$t$	$=$	$2.25 + 2 = 4.25$

$\frac{3}{2} x + 1$	$=$	$- \frac{2}{3} x + \frac{17}{4}$	$+ \frac{2}{3} x \| - 1$
	↓	Get $x$ to one side.
$\frac{3}{2} x + \frac{2}{3} x$	$=$	$\frac{17}{4} - 1$
	↓	Factor out $x$ and add the fractions.
$\frac{13}{6} x$	$=$	$\frac{13}{4}$	$: \frac{13}{6}$
$x$	$=$	$\frac{6}{4} = \frac{3}{2} = 1.5$

$y$	$=$	$\frac{3}{2} \cdot \frac{3}{2} + 1$
	$=$	$\frac{9}{4} + 1$
	$=$	$3.25$

Exercises: Distances, parallel and perpendicular lines

Setting up the line equation

Setting up the line equation

Setting up the line equation

Setting up the line equation

Distance between two parallel lines

Sketch

Line equation

Determine the intersection of d and g

Determine the distance between points S and T.

Result

Calculating the x-coordinate

﻿Calculating the y-coordinate

﻿

Calculating the $x$ -coordinate

Calculating the $y$ -coordinate