Exercises: Where the sine function comes from

How well do you know the sine function? Here, you can practice the investigation of sine functions with general parameters $a$ , $b$ and $c$ .

1
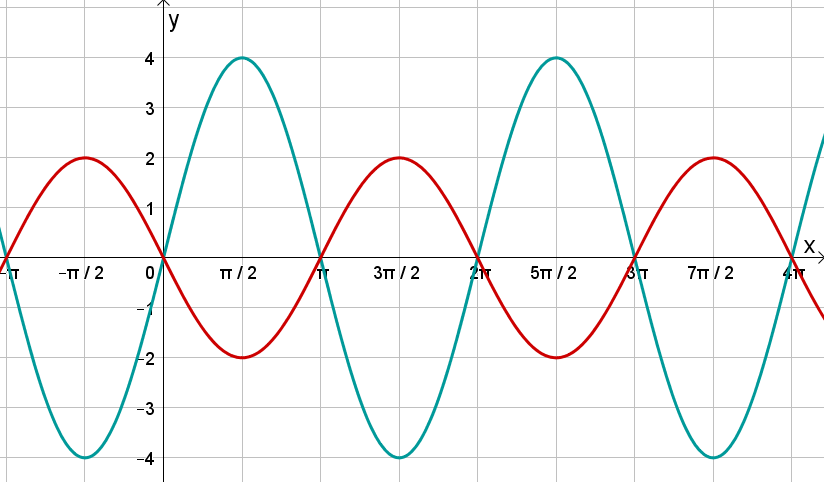
Verändere den Parameter $a$ und beobachte, wie sich der Funktionsgraph von $y = a \cdot s i n (x)$ , $x \in ℝ$ , gegenüber dem Graphen von $y = s i n (x)$ (hier in schwarz abgebildet) ändert!
Beantworte anschließend die Fragen.
Al hacer clic en la imagen o en el botón superior, aceptas que se cargará el contenido externo de provider . También los datos personales pueden ser transferidos a este servicio de acuerdo con nuestro Política de privacidad.
Für $a > 1$
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestreckt
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestaucht
stimmt der Funktionsgraph von $y = a \cdot s i n (x)$ mit dem Graphen von $y = s i n (x)$ überein

Für $0 < a < 1$
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestaucht
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestreckt
stimmt der Funktionsgraph von $y = a \cdot s i n (x)$ mit dem Graphen von $y = s i n (x)$ überein

Für $a = 1$
stimmt der Funktionsgraph von $y = a \cdot s i n (x)$ mit dem Graphen von $y = s i n (x)$ überein
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestreckt
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestaucht

Für $a < - 1$
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestreckt und an der $x -$ Achse gespiegelt
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestaucht und an der $x -$ Achse gespiegelt
wird der Funktionsgraph von $y = a \cdot s i n (x)$ nur an der $x -$ Achse gespiegelt

Für $- 1 < a < 0$
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestaucht und an der $x -$ Achse gespiegelt
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestreckt und an der $x -$ Achse gespiegelt
wird der Funktionsgraph von $y = a \cdot s i n (x)$ nur an der $x -$ Achse gespiegelt

Für $a = - 1$
wird der Funktionsgraph von $y = a \cdot s i n (x)$ nur an der $x -$ Achse gespiegelt
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestreckt und an der $x -$ Achse gespiegelt
wird der Funktionsgraph von $y = a \cdot s i n (x)$ in $y -$ Richtung gestaucht und an der $x -$ Achse gespiegelt

Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
der türkise Graph besitzt die Funktionsgleichung $y = 4 \cdot s i n (x)$
der rote Graph besitzt die Funktionsgleichung $y = - 2 \cdot s i n (x)$
der rote Graph besitzt die Funktionsgleichung $y = - 4 \cdot s i n (x)$
der türkise Graph besitzt die Funktionsgleichung $y = 3 \cdot s i n (x)$
der rote Graph besitzt die Funktionsgleichung $y = 2 \cdot s i n (x)$
2
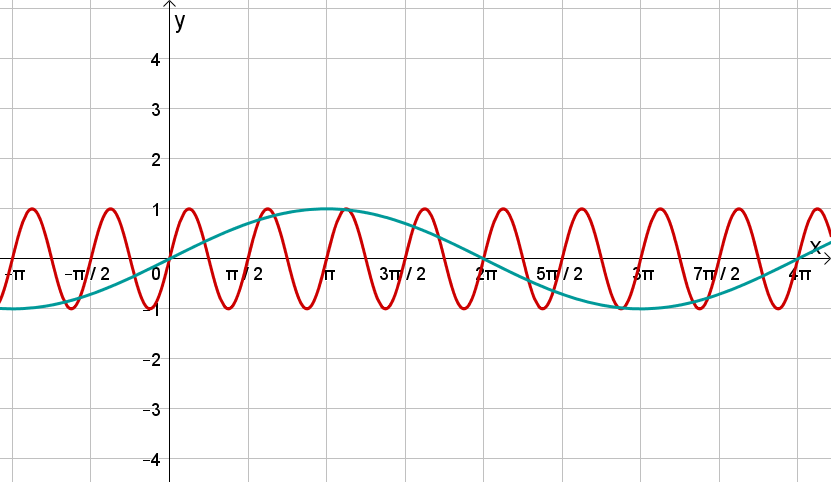
Verändere den Parameter $b$ und beobachte, wie sich der Funktionsgraph von $y = s i n (b \cdot x)$ , $x \in ℝ$ , $b > 0$ , gegenüber dem Graphen von $y = s i n (x)$ (hier in grau abgebildet) ändert!
Beantworte anschließend die Fragen.
Al hacer clic en la imagen o en el botón superior, aceptas que se cargará el contenido externo de provider . También los datos personales pueden ser transferidos a este servicio de acuerdo con nuestro Política de privacidad.
Für $b > 1$
wir der Funktionsgraph von $y = s i n (b \cdot x)$ in $x -$ Richtung gestaucht
wir der Funktionsgraph von $y = s i n (b \cdot x)$ in $x -$ Richtung gestreckt
stimmt der Funktionsgraph von $y = s i n (b \cdot x)$ mit dem von $y = s i n (x)$ überein

Für $0 < b < 1$
wir der Funktionsgraph von $y = s i n (b \cdot x)$ in $x -$ Richtung gestreckt
wir der Funktionsgraph von $y = s i n (b \cdot x)$ in $x -$ Richtung gestaucht
stimmt der Funktionsgraph von $y = s i n (b \cdot x)$ mit dem von $y = s i n (x)$ überein

Für $b = 1$
stimmt der Funktionsgraph von $y = s i n (b \cdot x)$ mit dem von $y = s i n (x)$ überein
wir der Funktionsgraph von $y = s i n (b \cdot x)$ in $x -$ Richtung gestreckt
wir der Funktionsgraph von $y = s i n (b \cdot x)$ in $x -$ Richtung gestaucht

Die Periode der Funktion mit der Funktionsgleichung $y = s i n (b \cdot x)$ , $b > 1$
wird kleiner als die Periode von $y = s i n (x)$
wird größer als die Periode von $y = s i n (x)$
ist gleich der Periode von $y = s i n (x)$

Die Periode der Funktion mit der Funktionsgleichung $y = s i n (b \cdot x)$ , $0 < b < 1$
wird größer als die Periode von $y = s i n (x)$
wird kleiner als die Periode von $y = s i n (x)$
ist gleich der Periode von $y = s i n (x)$

Die Periode der Funktion mit der Funktionsgleichung $y = s i n (b \cdot x)$ , $b = 1$
ist gleich der Periode von $y = s i n (x)$
wird größer als die Periode von $y = s i n (x)$
wird kleiner als die Periode von $y = s i n (x)$

Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
der türkise Graph besitzt die Funktionsgleichung $y = s i n (0,5 \cdot x)$
der rote Graph besitzt die Funktionsgleichung $y = s i n (4 \cdot x)$
der rote Graph besitzt die Periode $\frac{1}{2} π$
der türkise Graph besitzt die Periode $4 π$
der rote Graph besitzt die Funktionsgleichung $y = s i n (0,25 \cdot x)$
der türkise Graph besitzt die Funktionsgleichung $y = s i n (2 \cdot x)$
der rote Graph besitzt die Periode $π$
der türkise Graph besitzt die Periode $2 π$
3
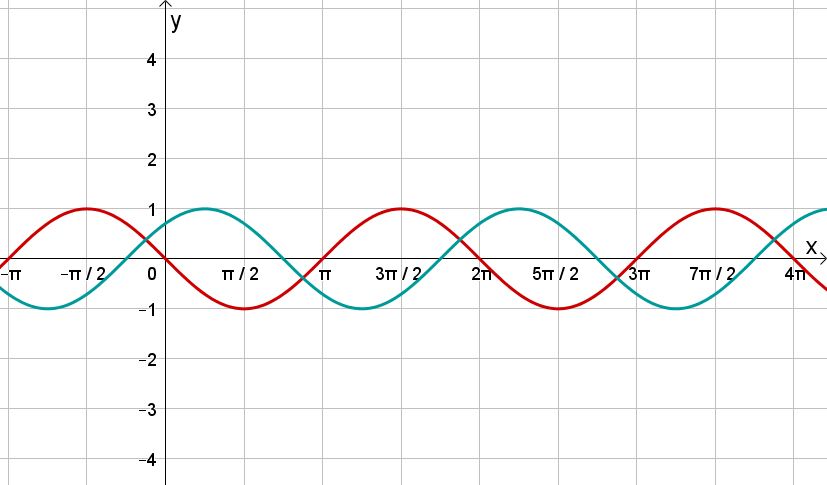
Verändere den Parameter $c$ und beobachte, wie sich der Funktionsgraph von $y = s i n (x + c)$ , $x \in ℝ$ , gegenüber dem Graphen von $y = s i n (x)$ (hier in grau abgebildet) ändert!
Beantworte anschließend die Fragen.
Al hacer clic en la imagen o en el botón superior, aceptas que se cargará el contenido externo de provider . También los datos personales pueden ser transferidos a este servicio de acuerdo con nuestro Política de privacidad.
Für $c > 0$
verschiebt sich der Funktionsgraph von $y = s i n (x + c)$ nach links
verschiebt sich der Funktionsgraph von $y = s i n (x + c)$ nach rechts
stimmt der Funktionsgraph von $y = s i n (x + c)$ mit dem von $y = s i n (x)$ überein

Für $c < 0$
verschiebt sich der Funktionsgraph von $y = s i n (x + c)$ nach rechts
verschiebt sich der Funktionsgraph von $y = s i n (x + c)$ nach links
stimmt der Funktionsgraph von $y = s i n (x + c)$ mit dem von $y = s i n (x)$ überein

Für $c = 0$
stimmt der Funktionsgraph von $y = s i n (x + c)$ mit dem von $y = s i n (x)$ überein
verschiebt sich der Funktionsgraph von $y = s i n (x + c)$ nach rechts
verschiebt sich der Funktionsgraph von $y = s i n (x + c)$ nach links

Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
der rote Graph besitzt die Funktionsgleichung $y = s i n (x - π)$
der türkise Graph besitzt die Funktionsgleichung $y = s i n (x + \frac{1}{4} π)$
der rote Graph besitzt die Funktionsgleichung $y = s i n (x + \frac{1}{2} π)$
der türkise Graph besitzt die Funktionsgleichung $y = s i n (x - \frac{1}{4} π)$