Mixed exercises: Trigonometric functions
How well do you know trigonometric functions? Practice on them with these exercises!
- 1
Berechne ohne Taschenrechner:
- 2
Berechne den Winkel im Intervall . Gib dein Ergebnis im Gradmaß an:
- 3
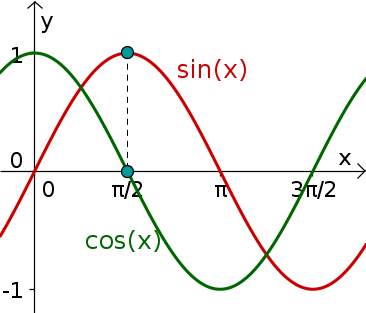
Es ist . Bestimme 3 weitere Winkel, die den gleichen Kosinuswert haben.
- 4
Prüfe, ob folgende Gleichungen für jede Stelle gelten:
- 5
Finde Beispiele für Phänomene in der Realität, die sich durch Sinus- und Kosinusfunktionen beschreiben lassen.
- 6
Prüfe, für welche im Intervall zwischen und die folgenden Gleichungen gelten:
Hinweis: Verwende den trigonometrischen Pythagoras .
- 7
Entscheide, ob die folgenden Beziehungen zwischen den trigonometrischen Funktionen richtig oder falsch sind.
- 8
Vereinfache den folgenden Term, bis nur noch darin vorkommt:
- 9
Löse für die folgende Gleichung nach auf:
- 10
Löse für die folgende Gleichung nach auf: