Exercises: Drawing graphs of linear functions
Draw the graph of the linear functions in a coordinate system!
For this task you need the following basic knowledge: Slope/Gradient of a line
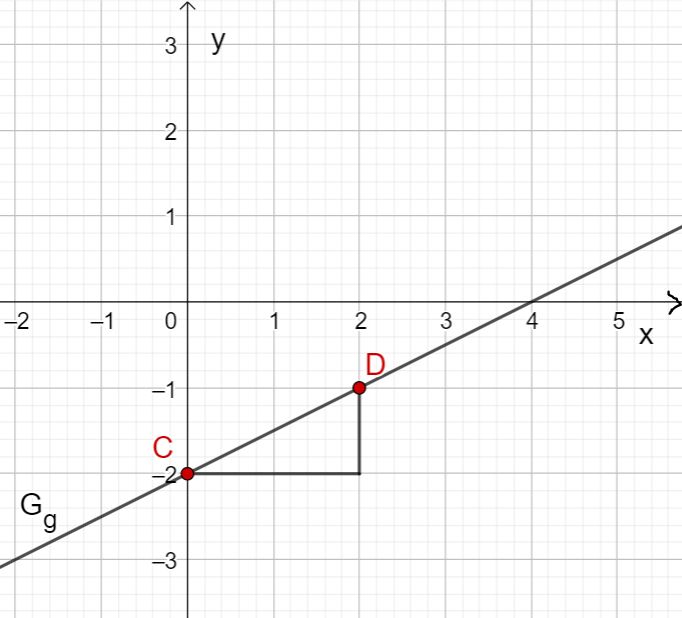
Drawing the linear function
First read off the -intercept and the slope from the function term of the linear function.
In this case:
You obtain a -intercept of and a slope of .
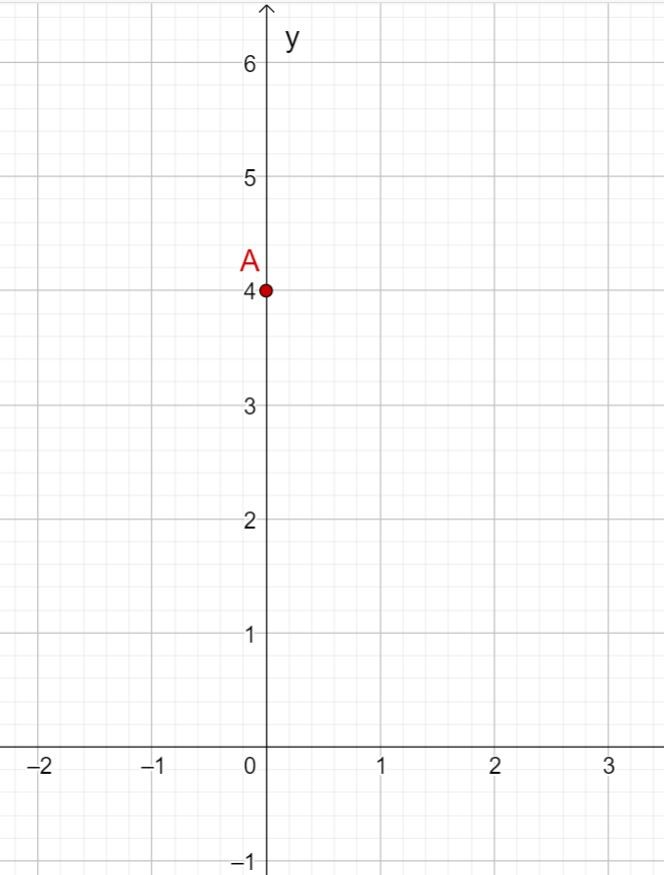
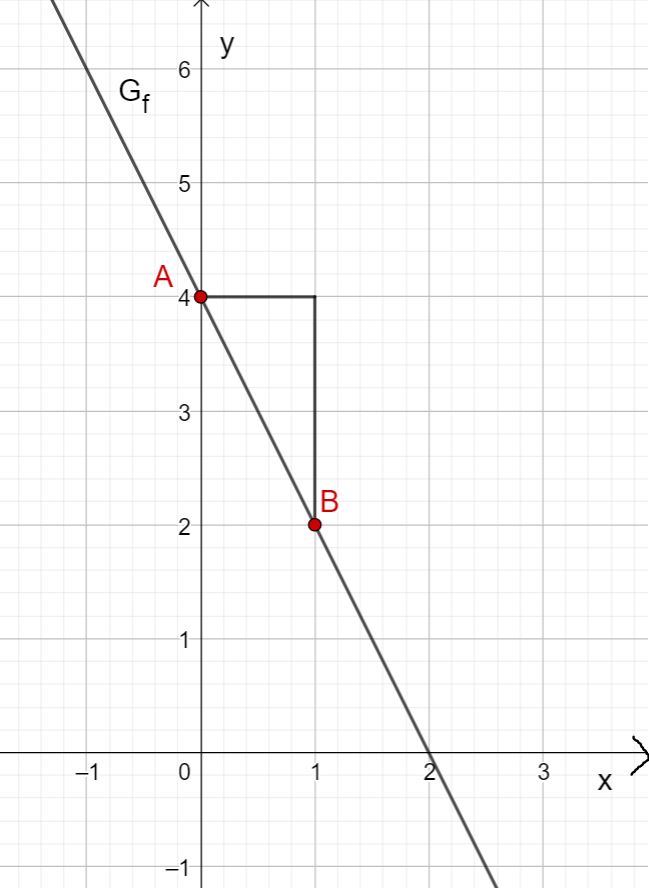
First draw the intersection with the -axis that results from the -axis intercept. This is at .
Then draw a gradient triangle using the gradient. To do this, go one length unit to the right and two length units down. This gives you the point . Now draw the straight line through points and .
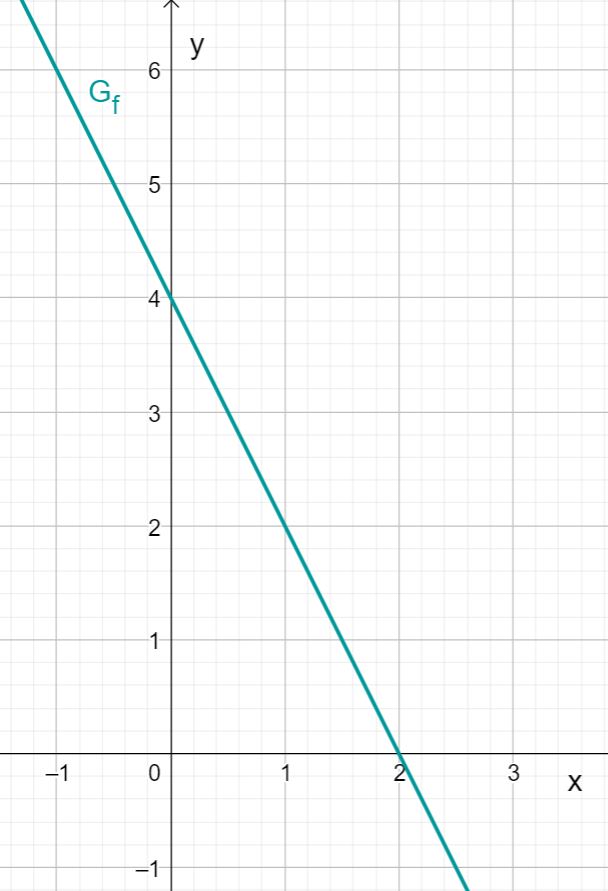
You obtain the graph of .
For this task you need the following basic knowledge: Slope/Gradient of a line
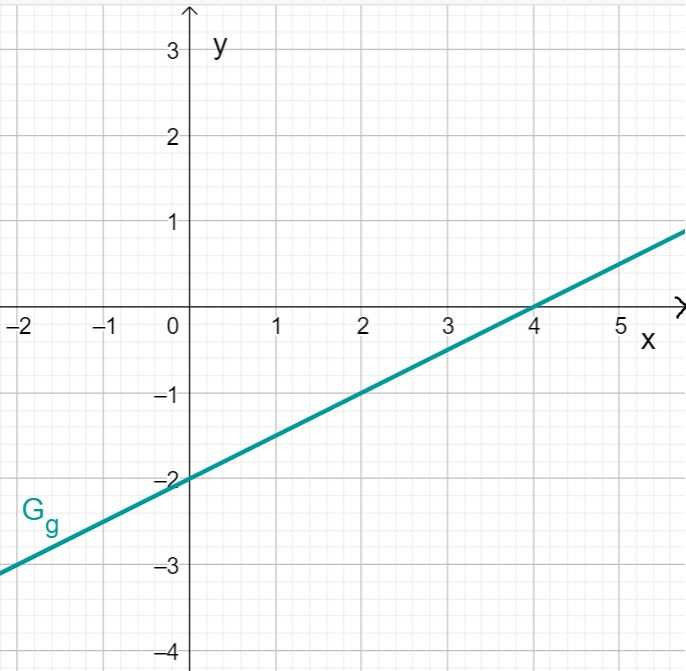
Drawing the linear function
First read off the -intercept and the slope from the function term of the linear function.
In this case:
You obtain a -intercept of and a slope of .
First draw the intersection with the -axis that results from the -axis intercept. This is at .
Then draw a gradient triangle using the gradient. To do this, go one length unit to the right and two length units down. This gives you the point . Now draw the straight line through points and .
You obtain the graph of .
For this task you need the following basic knowledge: Slope/Gradient of a line
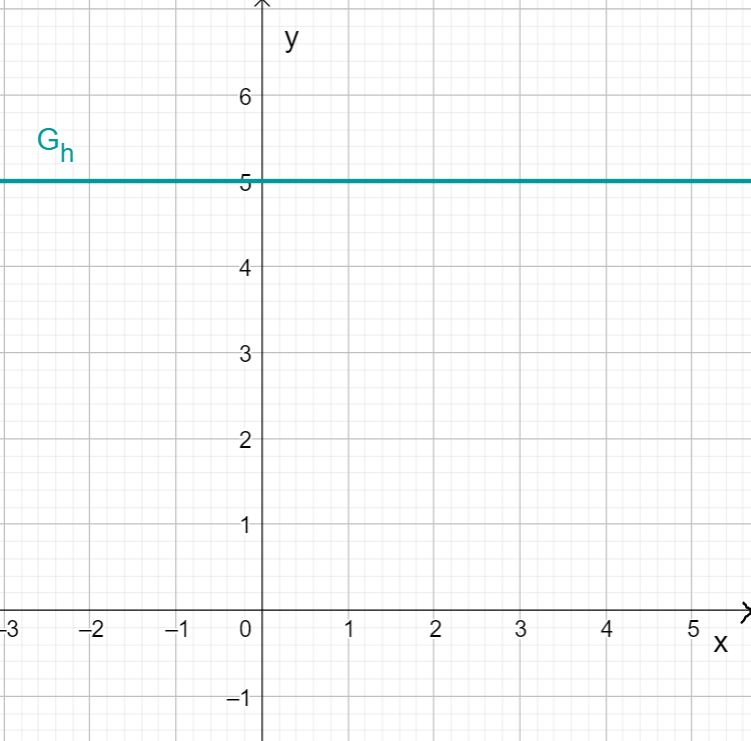
Drawing the linear function
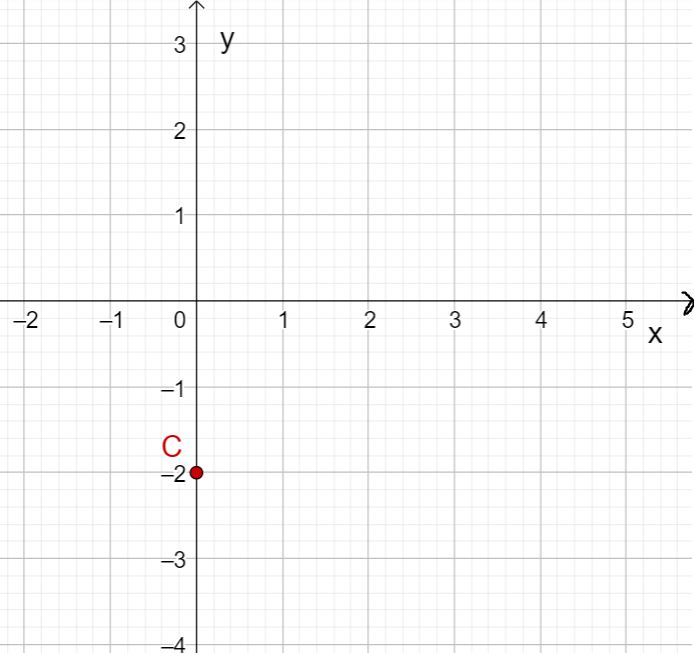
The function represents a special case of a linear function. The slope of is .
This means that the function value does not change regardless of the variable .
So if you draw the function value for each in a coordinate system, you get a straight line that runs parallel to the axis at the height .