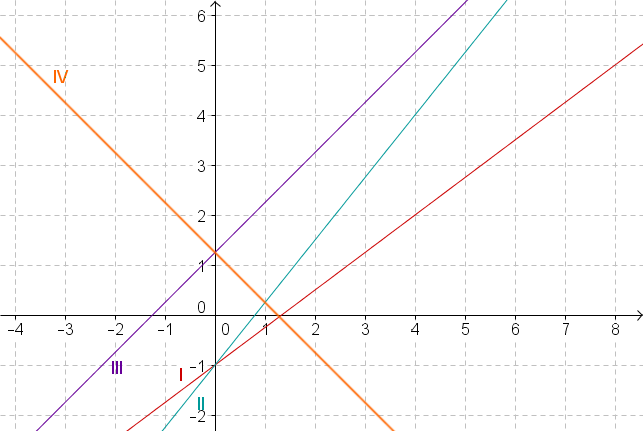
For this task you need the following basic knowledge: Line equation
Part 1:
You can read off the slope and the -axis intercept of this graph from the equation.
Given line equation:
First check for which functions the -intercept is by reading off the -value of each graph at the intersection with the -axis.
Now check which of the two graphs has the slope by moving one to the right from the point and checking which of the two -values increases by .
Only graph I and II have the -axis intercept so you can exclude any other graph.
Both graphs start at the point . Since the line we are looking for has the gradient , it also passes through the point
.
Only line II runs through this point.
Graph II is the one belonging to the given equation.
Part 2:
First look where the graph intersects the -axis to find the -axis intercept.
The line to be checked is III
Now read off how much the -value changes if you move one to the right starting from . This will give you the slope.
The -value of the point the line intersects the -axis is .
Therefore, .
The -value increases from to .
Thus the slope is .
Graph III has the line equation .