Exercises: Linear functions and line equations
- 1
Read off the slope from the graph.
For this task you need the following basic knowledge: Slope/Gradient of a line
You start from the -axis intercept (here ) and go to the right and upwards.
The slope is therefore:
Think about how you could draw a gradient triangle.
For this task you need the following basic knowledge: Slope/Gradient of a line
You start from the -axis intercept (here ) and go to the right and downwards.
The slope is therefore:
Think about how you could draw a gradient triangle.
For this task you need the following basic knowledge: Slope/Gradient of a line
You start from the -axis intercept (here ) and go to the right and upwards.
The slope is therefore:
Think about how you could draw a gradient triangle.
For this task you need the following basic knowledge: Slope/Gradient of a line
You start from the -axis intercept (here ) and go to the right and downwards.
The slope is therefore:
Think about how you could draw a gradient triangle.
For this task you need the following basic knowledge: Slope/Gradient of a line
You start from the -axis intercept (here ) and go to the right and upwards.
The slope is therefore:
Think about how you could draw a gradient triangle.
- 2
Consider the following graphs of linear functions:
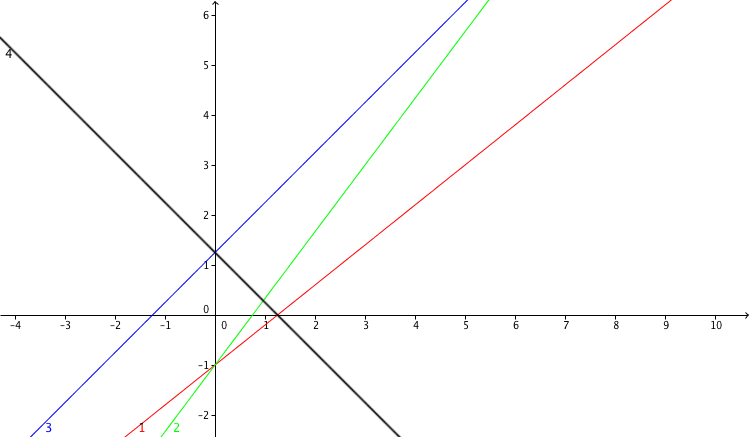
Which of the four graphs belongs to the equation ?
For this task you need the following basic knowledge: Funktionsgraphen linearer Funktionen zuordnen
Finde den Funktionsgraphen, der zur Funktionsgleichung gehört.
Bestimme daher zunächst den y-Achsenabschnitt.
Multipliziere und subtrahiere.
Gebe den y-Achsenabschnitt an.
Der y-Achsenabschnitt ist -1, der Graph schneidet also im Punkt (0,-1) die y-Achse. Somit können nur Graph 1 (rot) und Graph 2 (grün) zu der Funktion gehören.
Betrachte nun die Steigung der Graphen. Gib zuerst die Funktionsgleichung der Funktion an.
Gib die Steigung der Funktion an, indem du sie von der Geradengleichung abliest.
Graph 1 (rot)
Bestimme die Steigung von Graph 1 (rot), indem du ein Steigungsdreieck konstruierst. Lies dazu den Wert an der Stelle ab.
Für die Konstruktion eines Steigungsdreieck benötigst du einen zweiten Punkt. Gib dazu den schon berechneten Punkt des y-Achsenabschnitts an.
Berechne nun die Steigung gemäß .
Die Steigung des Graphen ist offenbar zu klein, als dass Graph 1 (rot) der zugehörige Funktionsgraph sein könnte.
Graph 2 (grün)
Bestimme die Steigung von Graph 2 (grün), indem du ein Steigungsdreieck konstruierst. Lies dazu den Wert an der Stelle ab.
Gib den Punkt des y-Achsenabschnitts an.
Für die Konstruktion eines Steigungsdreieck benötigst du einen zweiten Punkt. Gib dazu den schon berechneten Punkt des y-Achsenabschnitts an.
Ergebnis
Der zugehörige Graph ist Graph 2 (grün), da seine Steigung und sein y-Achsenabschnitt mit der Geradengleichung übereinstimmen.
Determine (approximately) the function term to the graph 3.
For this task you need the following basic knowledge: Linear function
You have to find the general form of a line equation:
The general equation of a straight line is .
-axis intercept
Determine the y-axis intercept of the function graph 3 (blue).
The -axis intercept is the function value at the intersection of the function graph with the -axis, i.e. the function value at .
Read off the point where the function graph intersects the -axis.
Wrote down the y-axis intercept t.
Slope
Determine the slope/gradient of the function graph 3 (blue) using a gradient triangle and give the expression for the slope.
Read off two points on graph 3 (blue) and then calculate the slope.
Now calculate the slope .
Result
The line equation of the function graph 3 (blue) is .
- 3
Determine the slope of the following straight lines.
For this task you need the following basic knowledge: Slope/Gradient of a line
The graph is rising. So only options and can be correct. If you go from the -axis intercept (here ) to the right by , you still have to go up by about to reach the straight line again.
The slope is therefore: .
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
For this task you need the following basic knowledge: Slope/Gradient of a line
You look for two points in the coordinate system whose coordinates you can read off easily. Here, for example, and . To get from to , you have to go to the right and down.
The slope is therefore:
Think about how you could draw a gradient triangle.
For this task you need the following basic knowledge: Slope/Gradient of a line
The line is falling. Therefore, the slope can only be negative. The only possible correct solutions are or .
If you move to the right in the coordinate system from the -axis intercept, you have to move less than down to meet the straight line again. So the answer cannot be correct.
If you look at the graph very very carefully, you get the result:
Think about how you could draw a gradient triangle.
For this task you need the following basic knowledge: Slope/Gradient of a line
The graph is rising, so the slope can only be positive. The answer options or or are therefore sensible at first glance.
Find a point on the straight line whose coordinates you can read off easily. For example, the point is suitable here. From here you have to go to the right and less than upwards to reach the straight line again. Therefore, only the answer option makes sense.
The slope is therefore:
Think about how you could draw a gradient triangle.
For this task you need the following basic knowledge: Slope/Gradient of a line
You start from the -axis intercept (here ) and go to the right and downwards.
The slope is therefore:
Think about how you could draw a gradient triangle.
- 4
Consider the following graphs for linear functions:
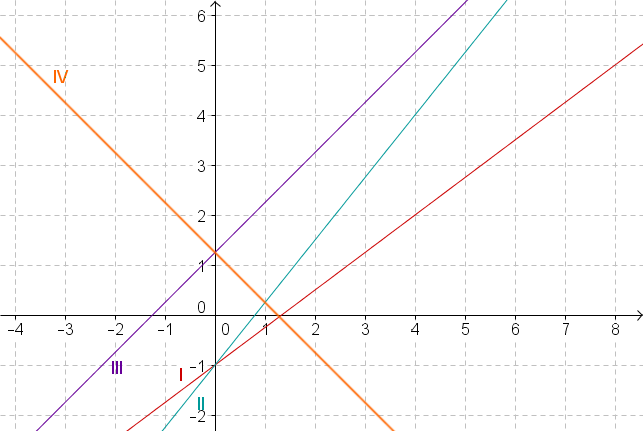
Which of the four graphs belongs to the equation
What is the equation of graph III?
For this task you need the following basic knowledge: Line equation
Part 1:
Given line equation:
First check for which functions the -intercept is by reading off the -value of each graph at the intersection with the -axis.
Now check which of the two graphs has the slope by moving one to the right from the point and checking which of the two -values increases by .
Only graph I and II have the -axis intercept so you can exclude any other graph.
Both graphs start at the point . Since the line we are looking for has the gradient , it also passes through the point .
Only line II runs through this point.
Graph II is the one belonging to the given equation.
Part 2:
First look where the graph intersects the -axis to find the -axis intercept.
The line to be checked is III
Now read off how much the -value changes if you move one to the right starting from . This will give you the slope.
The -value of the point the line intersects the -axis is .
Therefore, .
Set up the line equation.
The -value increases from to .
Thus the slope is .
Graph III has the line equation .
- 5
Determine the equation of the line that is parallel to the line and passes through the point .
h: ;
For this task you need the following basic knowledge: Slope/Gradient of a line
;
For the line to be parallel to , it must have the same gradient/slope.
The gradient of a line is called in the general line equation.
Setting up the equation
Plug and the point into the general line equation.
↓ solve for
Substitute and into the general line equation.
: ;
For this task you need the following basic knowledge: Slope/Gradient of a line
;
For the line to be parallel to , it must have the same gradient/slope.
The gradient of a line is called in the general line equation.
Setting up the equation
Plug and the point into the general line equation.
↓ solve for
Substitute and into the general line equation.
: ;
For this task you need the following basic knowledge: Slope/Gradient of a line
;
For the line to be parallel to , it must have the same gradient/slope.
The gradient of a line is called in the general line equation.
Setting up the equation
Plug and the point into the general line equation.
↓ solve for
Substitute and into the general line equation.
: ;
For this task you need the following basic knowledge: Slope/Gradient of a line
;
For the line to be parallel to , it must have the same gradient/slope.
The gradient of a line is called in the general line equation.
Setting up the equation
Plug and the point into the general line equation.
↓ solve for
Substitute and into the general line equation.
- 6
Determining function equations.
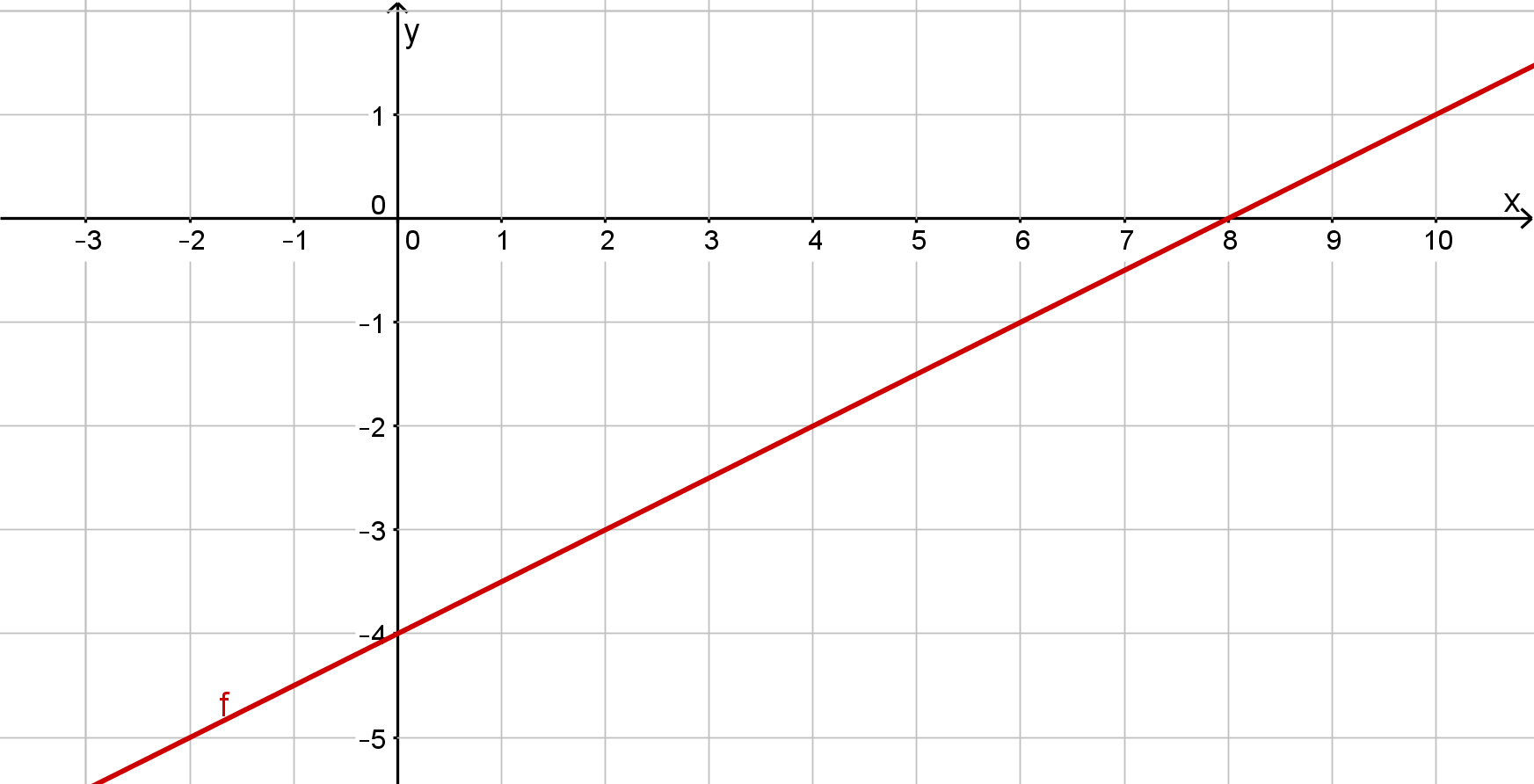
A line has the gradient and passes through the point . Determine the equation of the function , the points of intersection and draw the graph.
For this task you need the following basic knowledge: Linear function
Determining the function equaition
General line equation:
here
↓ plug into the general line equation.
↓ plug into
↓ solve for
↓ Plug into .
Determining the -axis intercept
What we are looking for is the so-called y-axis intercept (here: ), i.e. where and .
Since the general equation of a straight line is
, we have
.
Here
Intersection with the -axis at
Determining the -axis intercept
↓ We are looking for an with .
↓ You divide by a fraction multiply by the reciprocal.
Intersection with the -axis at
Plot
For this task you need the following basic knowledge: Linear function
Determining the function equation
General line equation:
↓ : -axis intercept
Plug into the general line equation.
↓ Plug into .
↓ multiply
↓ add
↓ Plug into .
Determining the axis intercepts
Set , to obtain the zeros of the function.
↓ You divide by a fraction multiply by the reciprocal.
↓ multiply
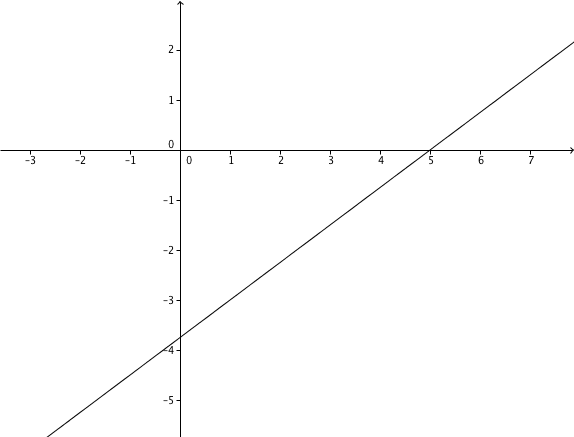
Intersection with the -axis at
The -axis intercept corresponds to the point of intersection with the -axis.
Intersection with the -axis at
Plot
For this task you need the following basic knowledge: Linear function
Determining the function equation
General line equation: Here
↓ : -axis intercept
Plug into the general line equation.
↓ Plug into .
↓ multiply
↓ subtract
↓ Plug into .
Determining the axis intercepts
Set , to obtain the zeros of the function.
↓ divide
Intersection with the -axis at .
The -axis intercept corresponds to the point of intersection with the -axis.
Intersection with the -axis at
Plot
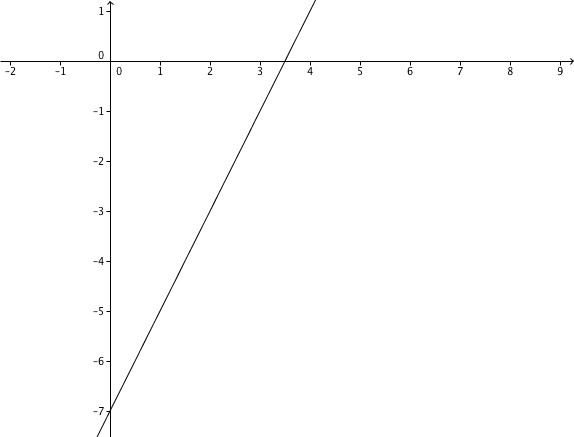
For this task you need the following basic knowledge: Linear function
Determining the function equation
General line equation:
↓ : -axis intercept
Plug into the general line equation
↓ Plug into .
↓ shorten by 2
↓ multiply
↓ Write 4 as a fraction with a 4 in the denominator
↓ subtract
↓ Setze t in f(x) ein.
Determining the axis intercepts
Set , to obtain the zeros of the function.
↓ divide
Intersection with the -axis at
The -axis intercept corresponds to the point of intersection with the -axis.
Here
Intersection with the -axis at .
Plot
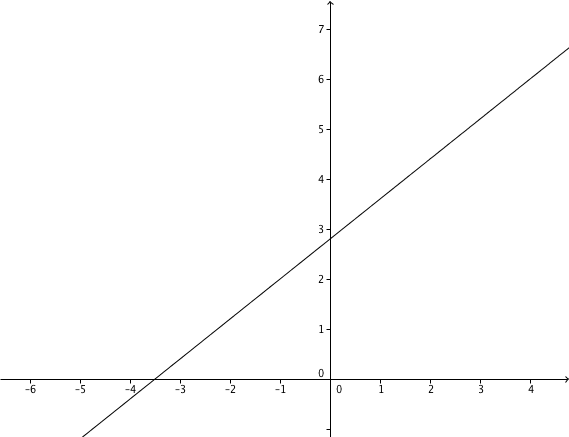
- 7
Determining the equation of a function.
A line passes through the points and . Determine the equation of the function , the points of intersection and draw the graph for the following values:
For this task you need the following basic knowledge: Linear function
Determining of the function equation
Substitute and into the general line equation .
Use the addition method.
Plug into .
Setze t und m in die allgemeine Geradengleichung ein.
Determining the axis intersection points
Set to determine the intersection with the -axis.
The intersection with the -axis is .
The point of intersection with the -axis corresponds to the -axis intercept
Drawing the graph
Connect either the two intersection points and or the two given points and .
Or choose one of these points and go one to the right and one up according to the slope and connect these two points.
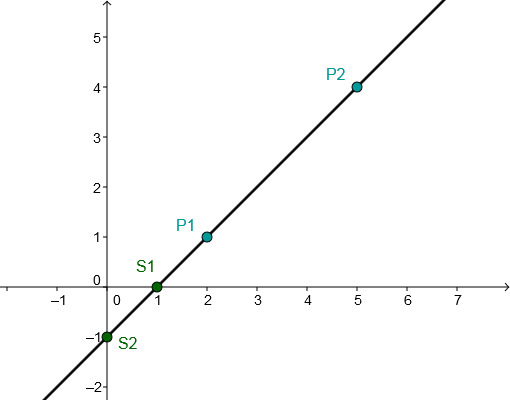
For this task you need the following basic knowledge: Linear function
Determining of the function equation
Substitute and into the general line equation .
Use the addition method.
↓ Plug into .
↓ Plug and into the general line equation.
Determining the axis intersection points
Set to determine the intersection with the -axis.
The intersection with the -axis is .
The point of intersection with the -axis corresponds to the -axis intercept
Drawing the graph
Connect either the two intersection points and or the two given points and .
Or choose one of these points and go one to the right and one up according to the slope and connect these two points.
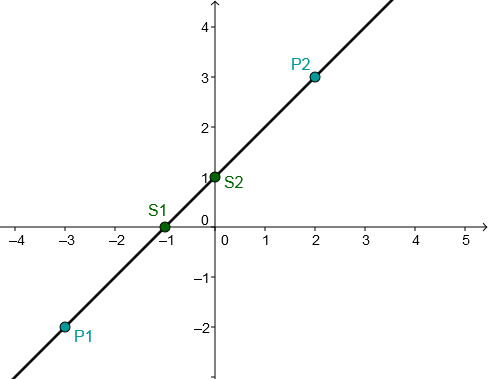
For this task you need the following basic knowledge: Linear function
Determining of the function equation
Substitute and into the general line equation .
Use the addition method.
Shorten the fractions.
Plug into .
Multiply.
Subtract.
Setze m und t in die allgemeine Geradengleichung ein.
Determining the axis intersection points
Set to determine the intersection with the -axis.
Divide the fractions
The intersection with the -axis is
The point of intersection with the -axis corresponds to the -axis intercept
Drawing the graph
Connect either the two intersection points and or the two given points and .
Or choose one of these points and go 3 to the right and 2 down according to the slope and connect these two points.
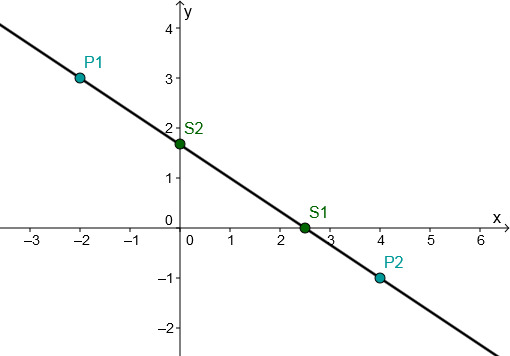
For this task you need the following basic knowledge: Linear function
Determining of the function equation
Substitute and into the general line equation .
Use the addition method.
Plug into .
Subtract.
Plug and into the general line equation.
Determining the axis intersection points
Set to determine the intersection with the -axis.
Divide the fractions. Multiply by the inverse.
Multiply.
The intersection with the -axis is .
The point of intersection with the -axis corresponds to the -axis intercept
Drawing the graph
Connect either the two intersection points and or the two given points and .
Or choose one of these points and go 7 to the right and 2 up according to the slope and connect these two points.
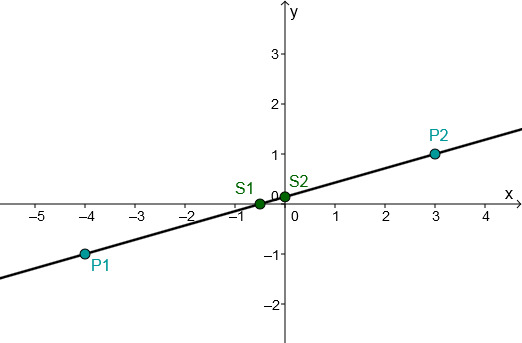
For this task you need the following basic knowledge: Linear function
Determining of the function equation
Substitute and into the general line equation .
Use the addition method.
Plug into .
Multiply.
Plug and into the general equation of a straight line.
Determining the axis intersection points
Set to determine the intersection with the -axis.
Divide the fractions. That means, multiply by the inverse.
Multiply.
The intersection with the -axis is
The point of intersection with the -axis corresponds to the -axis intercept
Drawing the graph
Connect either the two intersection points and or the two given points and .
Or choose one of these points and go 14 to the right and 11 down according to the slope and connect these two points.
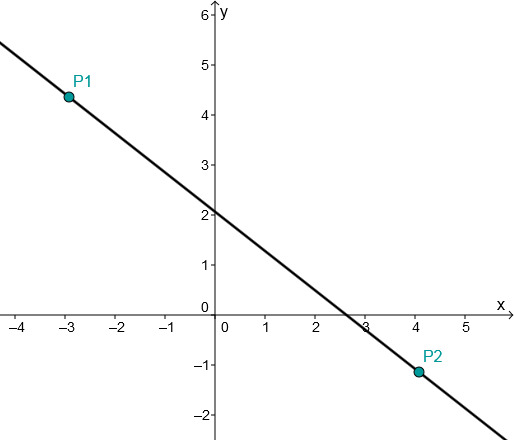
For this task you need the following basic knowledge: Linear function
Determining of the function equation
Substitute and into the general line equation .
Use the addition method.
Divide.
Plug into .
Multiply.
Plug and into the general equation of a straight line.
Determining the axis intersection points
Set to determine the intersection with the -axis.
The intersection with the -axis is
The point of intersection with the -axis corresponds to the -axis intercept
Drawing the graph
Connect either the two intersection points and or the two given points and .
Or choose one of these points and go 1 to the right and 0.8 up according to the slope and connect these two points.

- 8
Draw the following straight lines and give the function term.
has the slope and intersects the -axis at .
For this task you need the following basic knowledge: Linear function
Setting up the function term
Plug and into the general line equation .
Drawing the line
Select any point on the line, e.g. the -axis interception point . From there go 1 to the right and according to the slope upwards (alternatively, also the quadruple length to avoid fractions: 4 to the right and 3 upwards). Connect the two points to form a straight line.
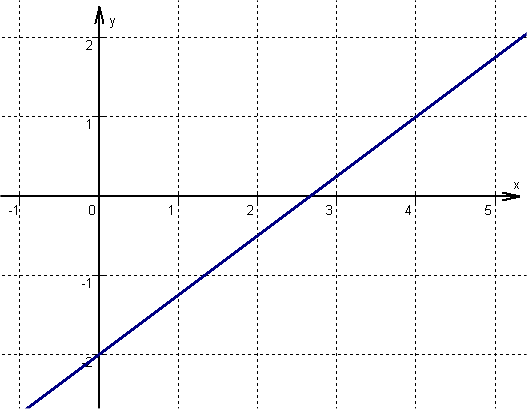
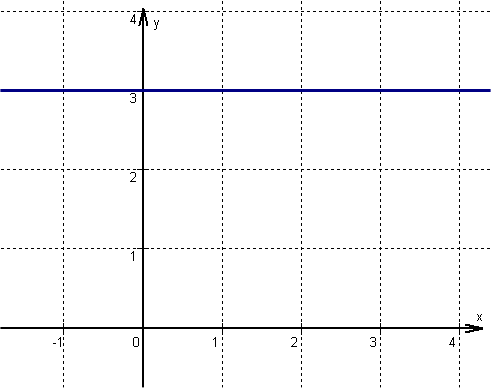
has the slope and intersects the -axis at .
For this task you need the following basic knowledge: Linear function
Setting up the function term
Plug and into the general line equation .
Drawing the line
The line runs through the -axis intercept parallel to the -axis because the line has a slope of 0.
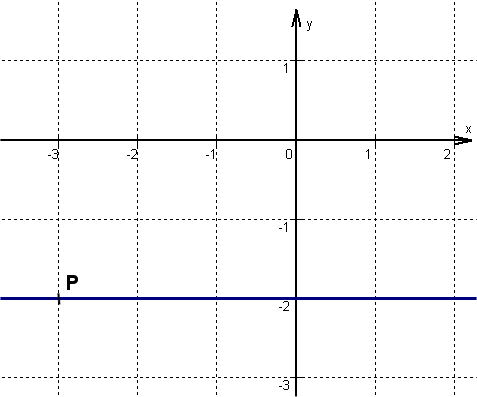
passes through the point and is parallel to the -axis.
For this task you need the following basic knowledge: Linear function
Setting up the function term
Since the line is parallel to the -axis, so its slope is .
The line goes through the point . Since the slope is 0, the line has the -value at .
Its -axis intercept is therefore
Plug and into the general line equation .
Drawing the line
The line runs through the -axis interception point and is parallel to the x-axis.
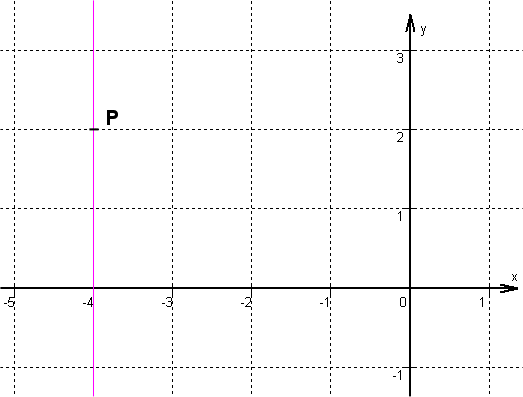
passes through the point and is parallel to the -axis.
For this task you need the following basic knowledge: Linear function
Setting up the function term
This straight line cannot be described by a function equation. The gradient would be infinitely large.
However, we can still draw the straight line.
Drawing the line
The line runs through the point and is parallel to the -axis.
- 9
Consider the four points , , , .
Draw the points - in a suitable coordinate system.
Determine the equation of the line passing through points -.
Give three more points that lie on the straight line.
For this task you need the following basic knowledge: Line equation
Coordinate system
1.

2.
Consider and .
Choose ... from A
and ... from B
Since the points - all lie on a common line, it is sufficient to select only two points (for example and ). With their help you determine the slope of the line. To do this, subtract the -coordinate of point from the -coordinate of point , and the -coordinate of point from the -coordinate of point .
Then determine the -axis intercept by inserting a point on the straight line (for example C) into the straight line equation and solving for .
Insert point into the line equation together with the previously calculated :
With this we have determined both and , so that our line equation is:
3.
Insert any three -values into the line equation to get the respective -value, e.g. , and .
This gives us the following three points , and :
and
- 10
Check that the straight line through and goes through the origin.
For this task you need the following basic knowledge: Linear function
Insert the two points into the general line equation:
Use the addition method.
Compute .
Plug into one of the two functions.
The line through and passes through the origin, since for the -value is equal to 0.
For this task you need the following basic knowledge: Linear function
Insert the two points into the general line equation:
For example, solve the linear system of equations with the addition method.
First multiply equation ) on both sides by
Compute
Plug into one of the two equations.
Plug and into the general line equation.
The line through and does not pass through the origin, because for the -value is equal to .
- 11
Determine the function equation.
A straight line has the -axis intercept and passes through the point . Determine the function equation and draw the graph.
For this task you need the following basic knowledge: Linear function
Determining the function equation
General line equation:
Substitute into the line equation.
Now plug the point into .
Solve for .
Plot:
For this task you need the following basic knowledge: Linear function
Determining the function equation
General line equation:
Substitute into the line equation.
Now plug the point into .
Solve for .
Plot:
- 12
Consider the following function graphs:

Which of the four graphs belongs to the equation `?
For this task you need the following basic knowledge: Line equation
The line equation is:
You can read off the slope and the -axis intercept of this graph from the equation.
First check which functions have a -intercept of by reading off the value of each graph at the interaction with the -axis.
Only graphs I and II have the intercept so you can exclude any other graph.
Now check which of the two graphs has the slope by moving one to the right from the point and checking which of the two -values increases by .
Both graphs start at the point . Since the straight line you are looking for has a slope of , it also passes through the point .
But only line II is running through this point.
Graph II is the one belonging to the given equation.
What is the equation to Graph III?
For this task you need the following basic knowledge: Line equation
Line to be checked: Graph III
First read off where the graph intersects the -axis to find the -axis intercept.
The -value of the point where the -axis is intersected amounts to .
Now read off by how much the -value changes when you go from , one to the right. This will give you the slope.
The -value increases from to .
Thus the slope is .
Set up the line equation.
⇒ Graph III has the equation
- 13
Consider the points , , , .
Draw the points - in a suitable coordinate system.
For this task you need the following basic knowledge: Line equation

Determine the equation of the line passing through points -.
For this task you need the following basic knowledge: Geradengleichung
Consider and .
Choose from : and and from : and .
Since the points - all lie on a common line, it is sufficient to select only two points (for example and ). With their help you determine the slope of the line. To do this, subtract the -coordinate of point from the -coordinate of point , and the -coordinate of point from the -coordinate of point .
Then determine the -axis intercept by inserting a point on the straight line (for example C) into the straight line equation and solving for .
Insert point into the line equation together with the previously calculated :
With this we have determined both and , so that our line equation is:
Give three more points that lie on the straight line.
For this task you need the following basic knowledge: Geradengleichung
Insert any three -values into the line equation to get the respective -value, e.g. , and .
This gives us the following three points , and :
and
- 14
Draw the following lines and determine the function term.
has the slope and intersects the -axis at .
For this task you need the following basic knowledge: Linear function
Seting up the function term
Insert and into the general line equation .
Draw the line
Select any point on the line, e.g. the -axis intercept (0|-2). Go from there 1 to the right and according to the slope upwards (alternatively, also the 4-fold length to avoid fractions: 4 to the right and 3 upwards). Connect the two points to get a straight line.

has a slope of 0 and intersects the -axis at 3.
For this task you need the following basic knowledge: Linear function
Seting up the function term
Insert and into the general line equation .
Draw the line
The line runs through the -axis intercept (0|3) parallel to the -axis because the straight line has a slope of 0.

passes through the point and is parallel to the -axis.
For this task you need the following basic knowledge: Linear function
Seting up the function term
Since the straight line is parallel to the -axis, its slope is 0 .
The line passes through the point . Since the slope is 0, the line has the -value -2 at .
Its -axis intercept is therefore at .
Insert and into the general line equation .
Draw the line
The line runs through the -intercept parallel to the -axis because the straight line has a slope of 0.

passes through the point and is parallel to the -axis.
For this task you need the following basic knowledge: Linear function
Seting up the function term
This straight line cannot be described by a function equation. The gradient would be infinitely large.
However, we can still draw the straight line.
Draw the line
The line runs through the point parallel to the -axis.

- 15
Determine the equation of the straight line through ...
the point and being parallel to the -axis.
For this task you need the following basic knowledge: Line equation
Parallel to the -axis, means that the slope is .
Plug and into the general line equation.
Assemble to a line equation.
the point and is parallel to the bisector of the 2nd quadrant (the diagonal pointing down).
For this task you need the following basic knowledge: Line equation
Parallel to the bisector of the 2nd quadrant means the line has the same slope as the bisector.
The slope of the bisector of the 2nd quadrant is -1
Plug into the straight line equation in order to calculate .
Plug and into the general equation of a straight line.
the point and is parallel to the -axis.
For this task you need the following basic knowledge: Line equation
Parallel to the -axis means that there is no function equation, since an -value is assigned an infinite number of -values.
The straight line can therefore only be described as the -value of .
the point and is parallel to the bisector of the 1st quadrant (the diagonal pointing up).
For this task you need the following basic knowledge: Line equation
The line being parallel to the bisector of the 1st quadrant means it has the same slope.
The slope of the bisector of the 1st quadrant is .
Substitute and into the general line equation and solve for .
Substitute and into the general line equation.
the origin and is parallel to the straight line with and .
For this task you need the following basic knowledge: Line equation
Passing through the origin means, the -axis intercept is .
Being parallel to the straight line means that the line has the same slope as .
Calculate the slope using the difference quotient .
Substitute and into the general line equation.





















