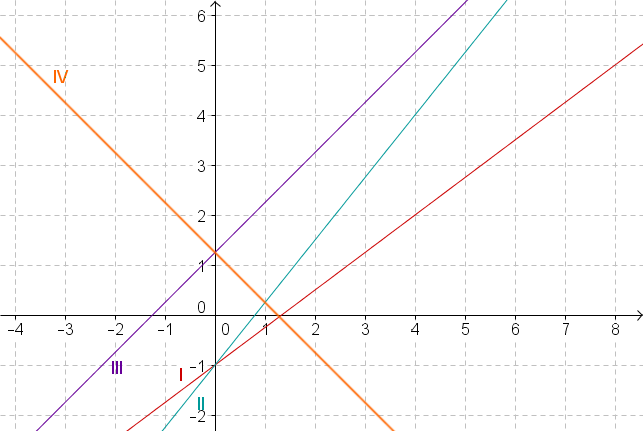
The line equation is: $y=\frac{5}{4}x-1y=\backslash frac54x-1$

You can read off the slope and the $yy$-axis intercept of this graph from the equation.

$m=\frac{5}{4}\text{}m=\backslash frac\{5\}\{4\}$

$t=-1t=-1$

First check which functions have a $yy$-intercept of $t=-1t=-1$ by reading off the $y-y-$value of each graph at the interaction with the $yy$-axis.

Only graphs I and II have the $y-y-$intercept $-1-1$ so you can exclude any other graph.

Now check which of the two graphs has the slope $m=\frac{5}{4}m=\backslash frac54$ by moving one to the right from the point $x=0x=0$ and checking which of the two $yy$-values increases by $\frac{5}{4}\backslash frac54$.

Both graphs start at the point $P(0;-1)P\backslash left(0;-1\backslash right)$. Since the straight line you are looking for has a slope of $\frac{5}{4}\backslash frac54$, it also passes through the point $(0+4\mathrm{\mid }-1+5)=(4\mathrm{\mid }4)(0+4|-1\; +5)=(4|4)$.

But only line II is running through this point.

$\Rightarrow \backslash Rightarrow$   Graph II is the one belonging to the given equation.

Line to be checked: Graph III

First read off where the graph intersects the $yy$-axis to find the $yy$-axis intercept.

The $yy$-value of the point where the $yy$-axis is intersected amounts to $y=1.25y=1.25$.

Now read off by how much the $yy$-value changes when you go from $x=0x=0$, one to the right. This will give you the slope.

The $yy$-value increases from $y=1.25y=1.25$ to $y=2.25y=2.25$.

Thus the slope is $m=\frac{2.25-1.25}{1}=\frac{1}{1}=1m=\backslash frac\{2.25-1.25\}\{1\}=\backslash frac11=1$ .

Set up the line equation.

⇒ Graph III has the equation $y=x+1.25y=x+1.25$