Math Functions Important types of functions and their properties Linear functions - Lines Exercises: Distances, parallel and perpendicular lines

Exercises: Distances, parallel and perpendicular lines

Calculate the distance of the parallel lines g: $y = - \frac{1}{2} x + 2$ and h: $y = - \frac{1}{2} x - 3$ .

Distance between two parallel lines

The shortest path between two parallel lines can be read off along a normal (=perpendicular line) of the two parallel lines .

The distance of the straight lines is equal to the distance between the two intersection points of the normal line with the parallel lines .

Sketch

The construction looks as follows:

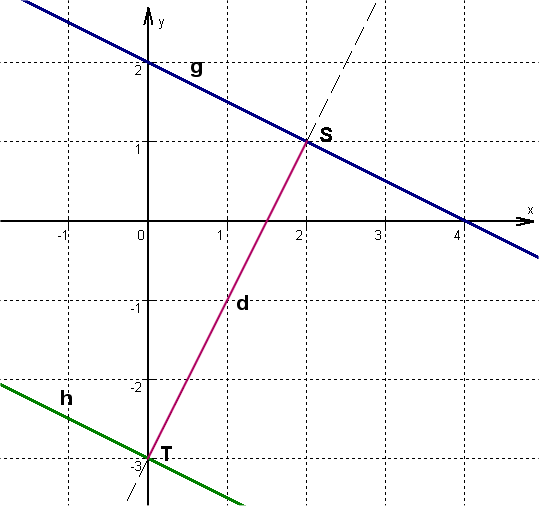
Graph Geraden Parallelen Abstand zwischen den Parallelen

Line equation

Establish the line equation of the normal line d.

First calculate the slope.

$m_{d} \cdot m_{g}$	$=$	$- 1$	$: m_{g}$
$m_{d}$	$=$	$\frac{- 1}{m_{g}}$
	↓	Plug in the slope $m_{g} = - \frac{1}{2}$
$m_{d}$	$=$	$\frac{- 1}{- \frac{1}{2}}$
	↓	Simplify the right-hand side
$m_{d}$	$=$	$- 2$

Now set up the line equation.

For this, you need a point $T$ , which lies on line h. For instance, you may take the $y$ -axis intercept of $h (x)$ , which is $T (0 | - 3)$ . But any other point is also correct.

Plug $T (0 | - 3)$ and $m_{d}$ into the general line equation for d to get the parameter $t$ .

$- 3$	$=$	$2 \cdot (0) + t$
	↓	multiply out
$t$	$=$	$- 3$
	↓	Plug $t$ and $m_{d}$ into the general line equation.
$y$	$=$	$2 x - 3$

Determine the intersection of d and g

First calculate the $x$ -coordinate of the intersection point $S$ .

Normal line d: $y = 2 x - 3$

Paralle line g: $y = - \frac{1}{2} x + 2$

Equate both function equations:

$2 x - 3$	$=$	$- \frac{1}{2} x + 2$	$+ 3$
$2 x$	$=$	$- \frac{1}{2} x + 5$	$+ \frac{1}{2} x$
$\frac{5}{2} x$	$=$	$5$	$: \frac{5}{2}$
$x$	$=$	$2$

Now calculate the $y$ -coordinate of the intersection point $S$ .

$y$	$=$	$2 x - 3$
	↓	Plug in x = 2 .
$y$	$=$	$2 \cdot 2 - 3$
	↓	compute
$y$	$=$	$1$

Hence the point $S$ has the following coordinates:

$\Rightarrow$ $S (2 | 1)$

Determine the distance between points S and T.

Determine the distance in $x$ -direction.

$T (0 | - 3)$ , $S (2 | 1)$

Calculate the difference of the $x$ -values of $S$ and $T$ .

$Δ x = 2 - 0 = 2$

Determine the distance in $y$ -direction.

$T (0 | - 3)$ , $S (2 | 1)$

Calculate the difference of the $y$ -values.

$Δ y = 1 - (- 3) = 4$

Determine the distance in a direct line between the points.

$Δ x = 2$

$Δ y = 4$

This is done by the Pythagoraen Theorem:

$d^{2}$	$=$	$2^{2} + 4^{2}$
	↓	compute both squares
$d^{2}$	$=$	$4 + 16$
	↓	add
$d^{2}$	$=$	$20$
	↓	take the root
$d^{}$	$=$	$\sqrt{20}$

If you enter $\sqrt{20}$ into a calculator and round the result to two decimal places, you get:

$d = \sqrt{20} \approx 4.47$

Result

The distance between the two lines is $d = \sqrt{20} \approx 4.47$ .

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org