Draw the graphs of the following lines including the point of intersection with the y-axis and a gradient triangle. Calculate the point of intersection with the x-axis and check the result using the graph.
f(x)=2x−5
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
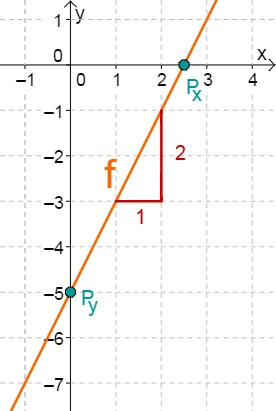
f(x)=2x−5
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−5)
⇒mf=2
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
2x−5 = 0 +5 2x = 5 :2 x0 = 2.5 ⇒Px(2.5∣0)
Do you have a question?
f(x)=−x−3
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
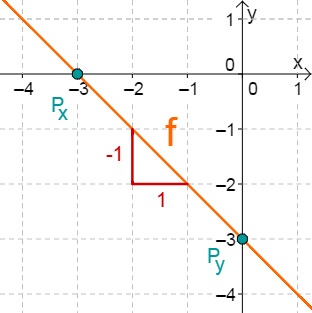
f(x)=−x−3
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−3)
⇒mf=−1
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−x−3 = 0 +x −3 = x0 ⇒Px(−3∣0)
Do you have a question?
f(x)=21x+1
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
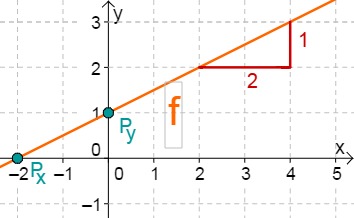
f(x)=21x+1
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣1)
⇒mf=21
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
21x+1 = 0 −1 21x = −1 ⋅2 x0 = −2 ⇒Px(−2∣0)
Do you have a question?
f(x)=−21x−2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
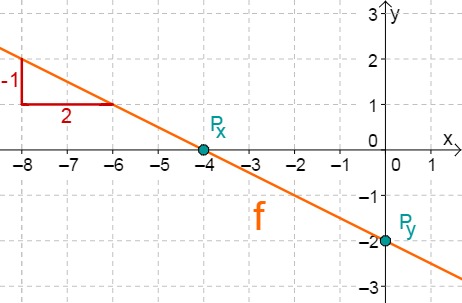
f(x)=−21x−2
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−2)
⇒mf=−21
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−21x−2 = 0 +2 −21x = 2 ⋅(−2) x0 = −4 ⇒Px(−4∣0)
Do you have a question?
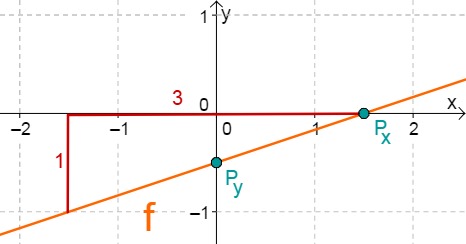
f(x)=31x−21
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=31x−21
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0−21)
⇒mf=31
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
31x−21 = 0 +21 31x = 21 ⋅3 x0 = 23 ⇒Px(23∣0)
Do you have a question?
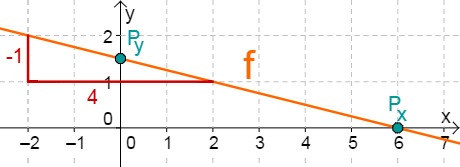
f(x)=−41x+23
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=−41x+23
First read off the y-axis intercept and the slope from the function equation.
⇒Py(023)
⇒mf=−41
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−41x+23 = 0 −23 −41x = −23 ⋅(−4) x0 = 6 ⇒Px(6∣0)
Do you have a question?
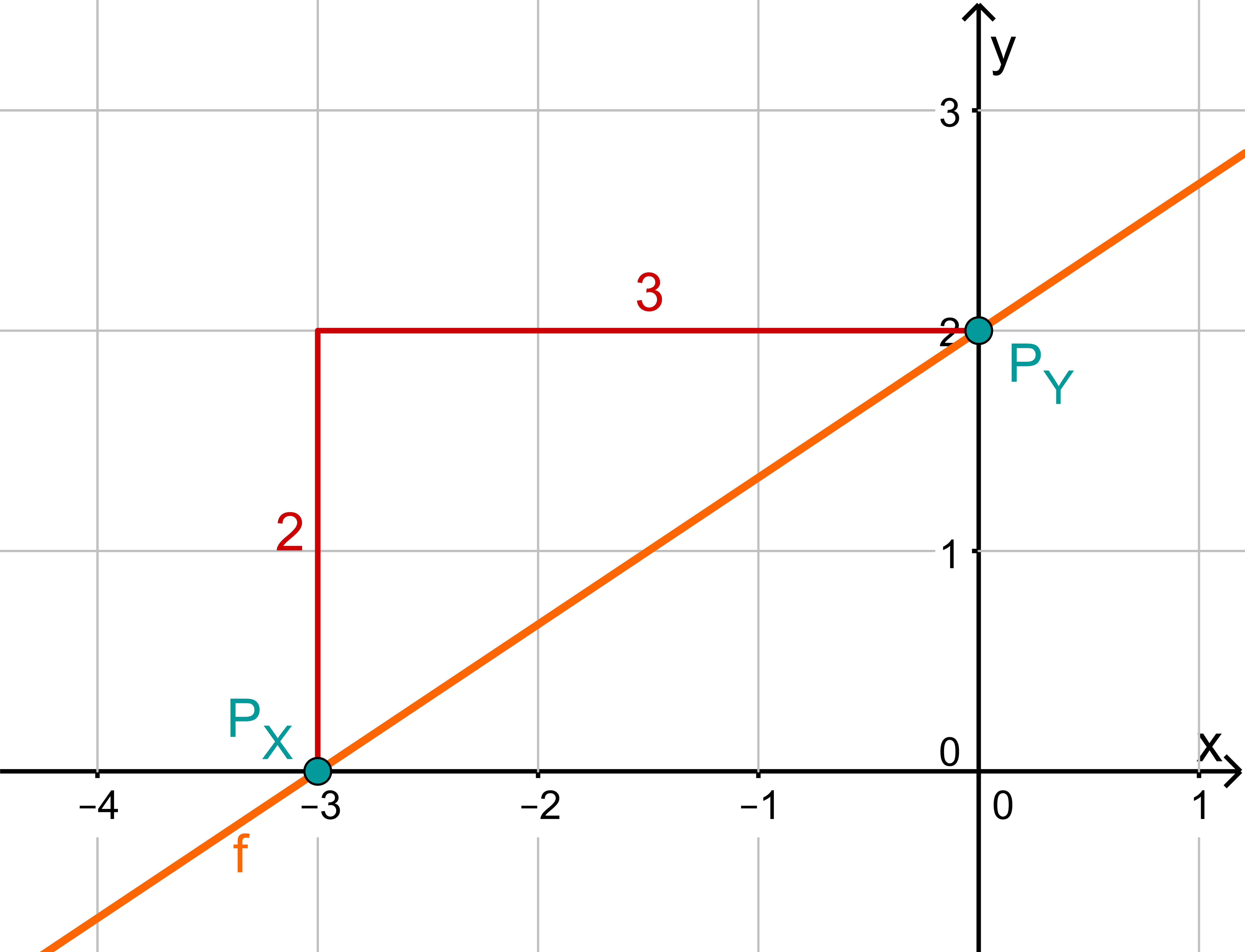
f(x)=32x+2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=32x+2
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣2)
⇒mf=32
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
32x+2 = 0 −2 32x = −2 :32 x0 = −3 ⇒Px(−3∣0)
Do you have a question?
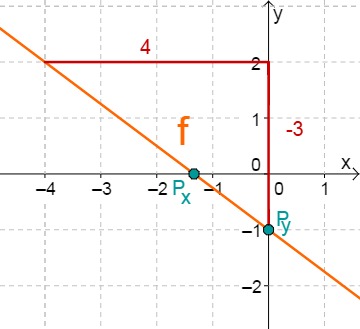
f(x)=−43x−1
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=−43x−1
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−1)
⇒mf=−43
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−43x−1 = 0 +1 −43x = 1 :(−43) x0 = −34 ⇒Px(−34∣0)
Do you have a question?
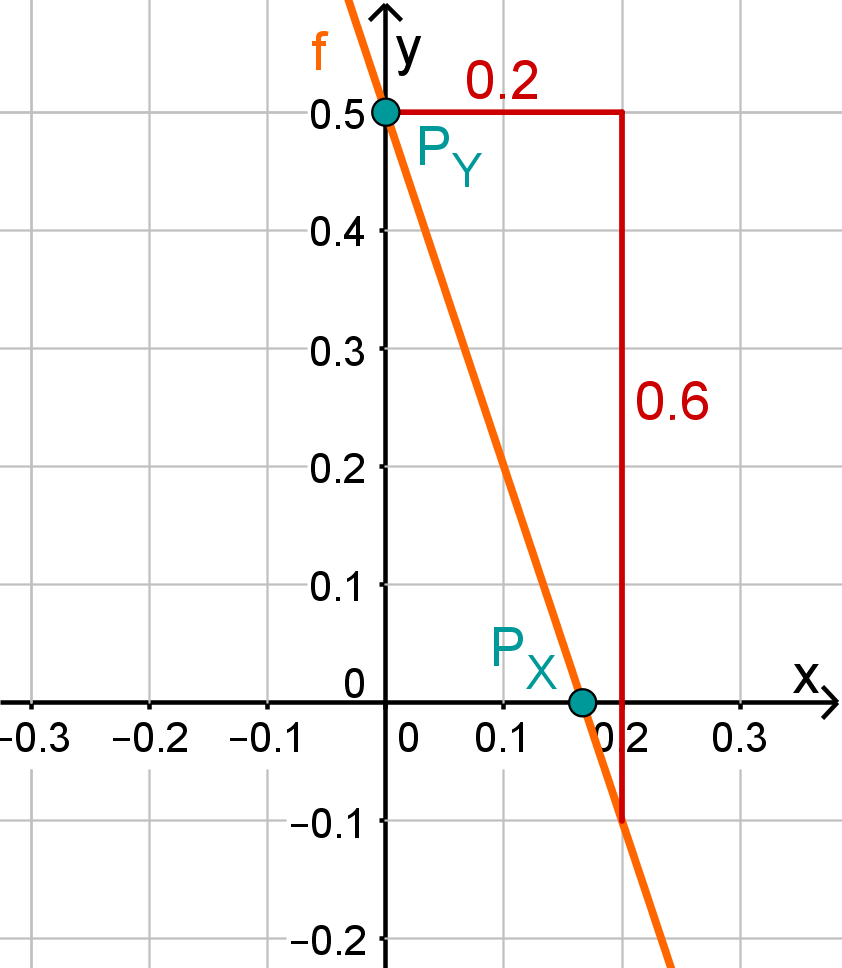
f(x)=−3x+105
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=−3x+105
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0105)
⇒mf=−3
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−3x+105 = 0 −105 −3x = −21 :(−3) x0 = −61 ⇒Px(61∣0)
Do you have a question?
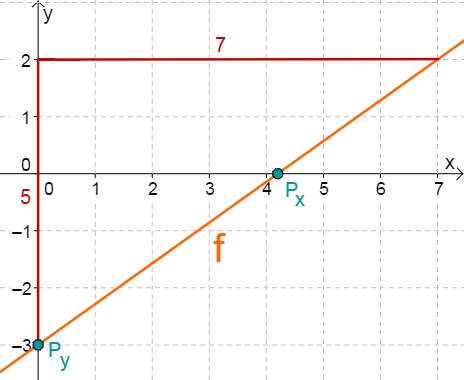
f(x)=75x−412
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=75x−412=75x−3
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−3)
⇒mf=75
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
75x−3 = 0 +3 75x = 3 :75 x0 = 521 ⇒Px(521∣0)
Do you have a question?
This content is licensed under
CC BY-SA 4.0 → Info
