Exercises: Linear functions, zeros, axis intercepts
- 1
Read off the y-axis intercept from the graph.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣0), so y=0.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣3), so y=3.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣−4), so y=−4.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣−3), so y=−3.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣4), so y=4.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣5), so y=5.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣2), so y=2.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣3), so y=3.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣−1), so y=−1.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The y-axis intercept is the y-value of the intersection with the y-axis S(0∣−4), so y=−4.
Do you have a question?
You get the y-axis intercept by looking at the intersection of the line with the y-axis.
- 2
Read off the zero from the graph.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Calculating zeros
The zero is the x-value of the intersection of the line with the x-axis N(0∣0), so x=0.
Do you have a question?
You determine the zero by looking at the intersection of the line with the x-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Calculating zeros
The zero is the x-value of the intersection of the line with the x-axis N(1∣0), so x=1.
Do you have a question?
You determine the zero by looking at the intersection of the line with the x-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Calculating zeros
The zero is the x-value of the intersection of the line with the x-axis (2∣0), so x=2.
Do you have a question?
You determine the zero by looking at the intersection of the line with the x-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Calculating zeros
The zero is the x-value of the intersection of the line with the x-axis N(3∣0), so x=3.
Do you have a question?
You determine the zero by looking at the intersection of the line with the x-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Calculating zeros
The zero is the x-value of the intersection of the line with the x-axis N(3∣0), so x=3.
Do you have a question?
You determine the zero by looking at the intersection of the line with the x-axis.
The zero is the x-value of the intersection of the line with the x-axis N(7∣0), so x=7.
Do you have a question?
You determine the zero by looking at the intersection of the line with the x-axis.
- 3
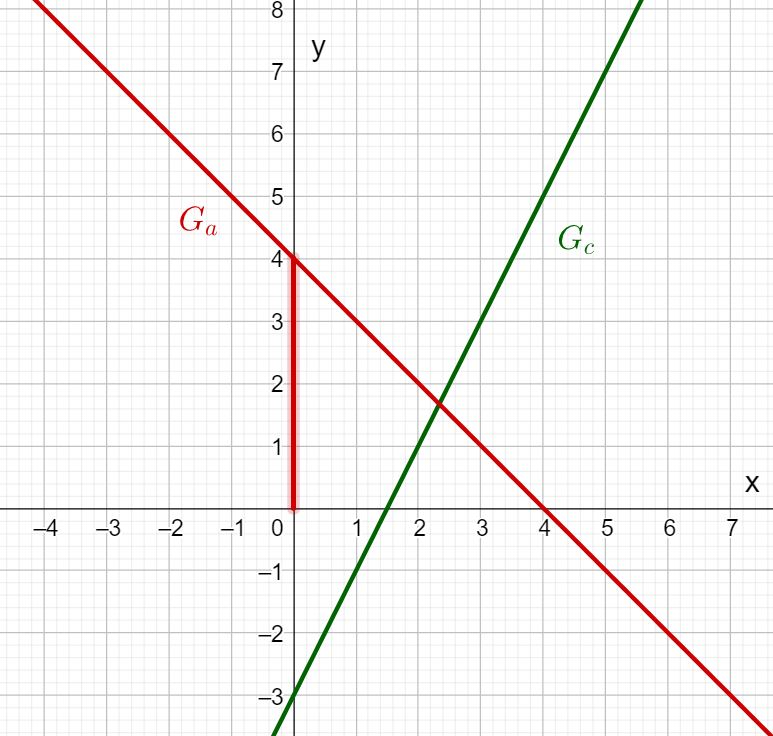
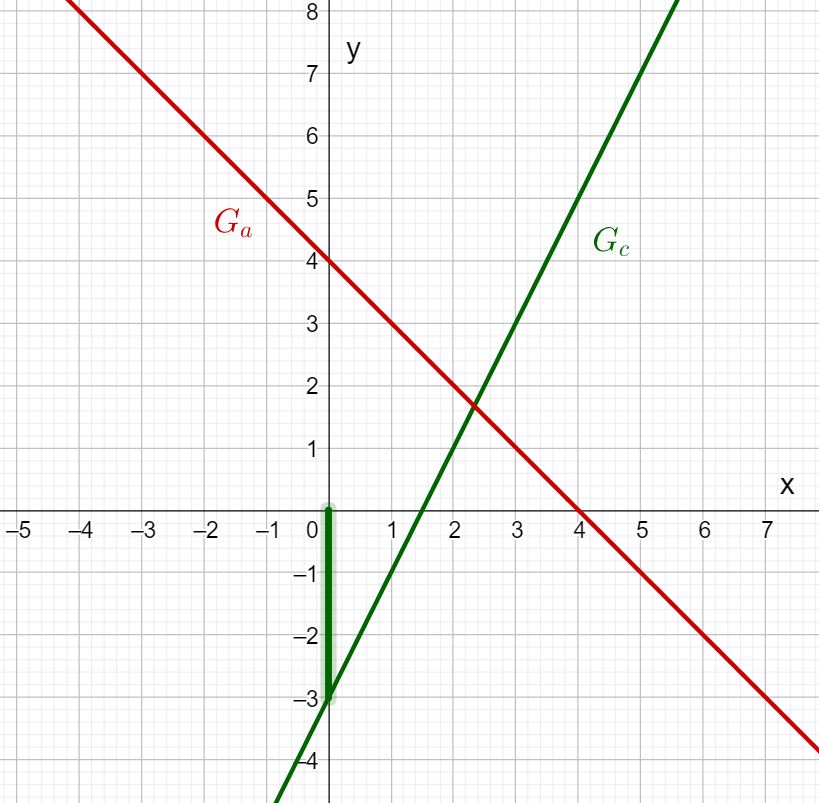
Look at the graphs of the functions a(x) and c(x).
Read off the y-axis intercept and the slope of the lines and enter them in the boxes!
Can you work out the function term from this?
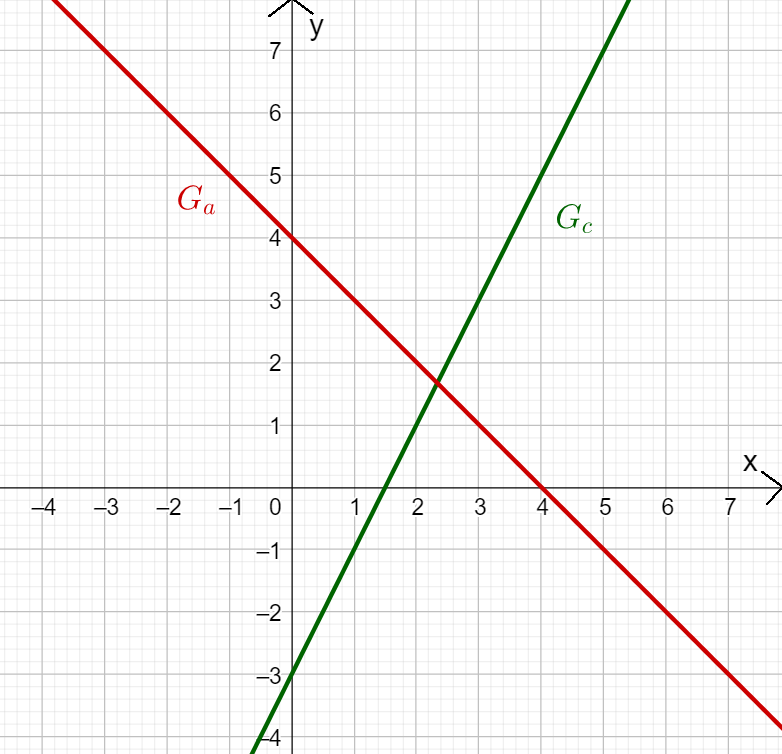
What is the y-axis intercept of a(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line equation in analytic geometry
Determining the y-axis intercept
You determine the y-axis intercept by looking at the intersection of the straight line with the y-axis. In this case:
The y-axis intercept is the y-value of the intersection point (0/4), i.e. 4.
Do you have a question?
Notice where the straight line Ga intersects the y-axis.
Determine the intersection.
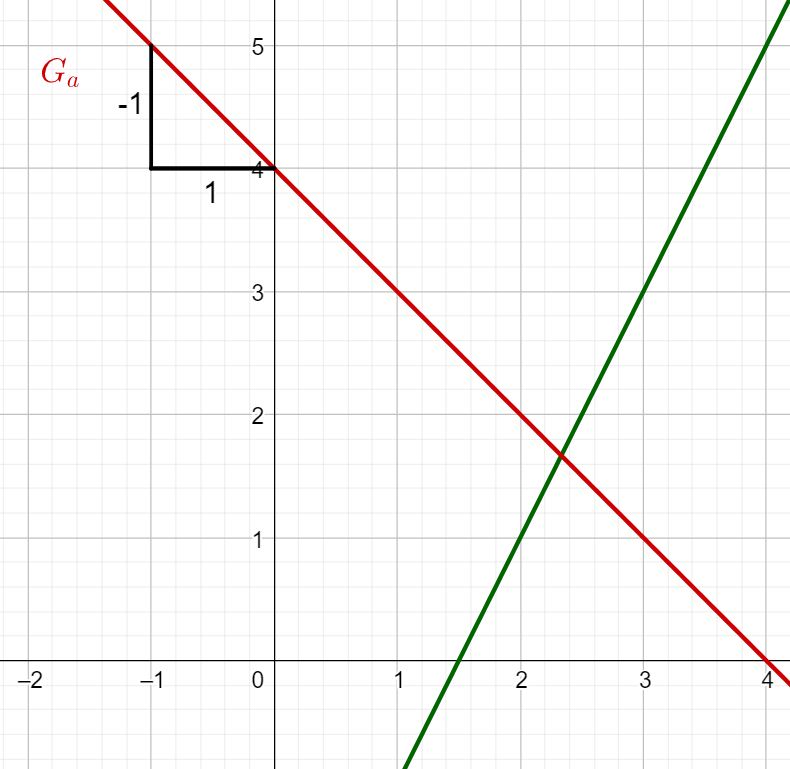
What is the slope of a(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Slope/Gradient of a line
Determining the slope
The easiest way to determine the slope of a straight line is to use a gradient triangle.
In the case of Ga:
You have to go one length unit to the right and one length unit down.
Therefore, you get the slope m=−1
Do you have a question?
Pick a gradient triangle (see below).
Then determine the slope.
What is the function term of a(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Setting up the function term
The function term of a linear function takes the form:
y=mx+tHere m is the slope and t the y-axis intercept.
If you insert the values from the previous sub-tasks, you get:
y=−1⋅x+4Simplified, that is:
y=−x+4The function equation of Ga is thus:
a(x)=−x+4.
Do you have a question?
Recap the basic knowledge about linear functions.
Put your previous values into the function (see below for a more detailed explanation).
What is the y-axis intercept of c(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line equation in analytic geometry
Determining the y-axis intercept
You determine the y-axis intercept by looking at the intersection of the straight line with the y-axis. In this case:
Therefore, the y-axis intercept of Gc is −3.
Do you have a question?
Notice where the straight line Gc intersects the y-axis.
Determine the intersection.
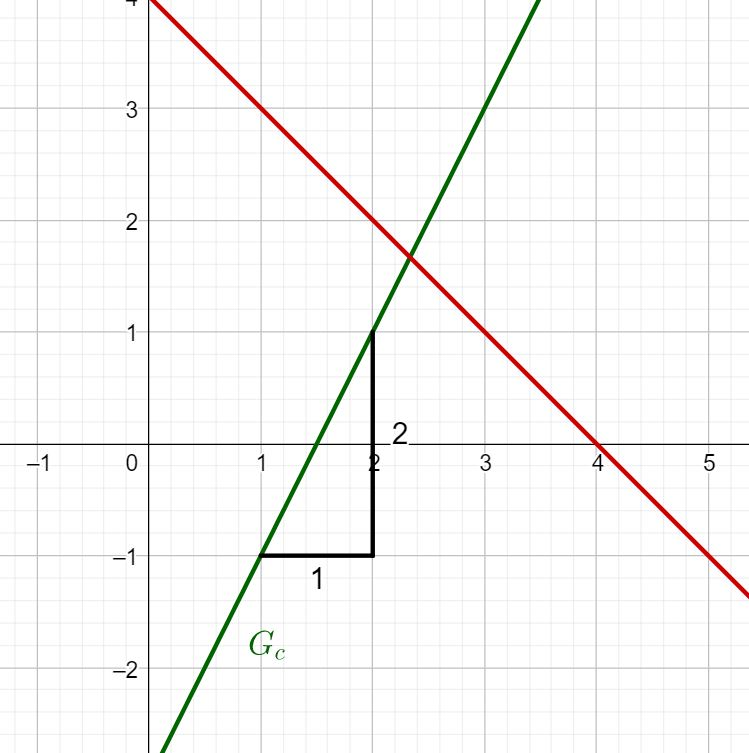
What is the slope of c(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Slope/Gradient of a line
Determining the slope
The easiest way to determine the slope of a straight line is to use a gradient triangle.
In the case of Gc:
You have to go one length unit to the right and two length units up.
Therefore, you get the slope: m=2
Do you have a question?
Pick a gradient triangle (see below).
Then determine the slope.
What is the function term of c(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Setting up the function term
The function term of a linear function takes the form:
y=mx+tHere m is the slope and t the y-axis intercept.
If you insert the values from the previous sub-tasks, you get:
y=2⋅x−3The functional equation of Gc is thus:
c(x)=2x−3Do you have a question?
Recap the basic knowledge about linear functions.
Put your previous values into the function (see below for a more detailed explanation).
- 4
Consider the lines g:y=2x−3 and h:y=−0.5x+3 .
Check whether the points A(1∣−1), B(0.5∣1.5), C(−6∣5), D(−102∣55) and E(45∣87) are on either of both lines.
Complete the coordinates so that the points lie on h: P(5∣?) , Q(−3.5∣?) , R(?∣12) , S(?∣−7,5).
Show that T(2.4∣1.8) lies on both lines. What does this mean?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line equation
Part 1
Drawing a sketch
Select any point on the straight line, e.g. the y-axis intercepts (0∣−3) and (0∣3). Go from there 1 unit to the right and, corresponding to the slopes, mg=2 upwards and mh=−0.5 downwards. Connect the two points to form a straight line.
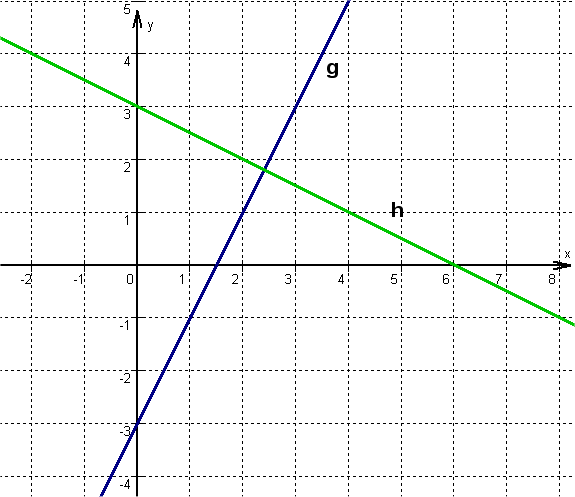
If you look at the straight line and, for example, the position of point A, you will see that it will hardly lie on the straight line h, but probably on g. Similarly, you can decide for other points whether a mathematical check is worthwhile: Point D(−102/55) can only lie on h, for example.
Check by computation
A(1∣−1) on g
Put the coordinates of the points into the equation in question. So set y=−1 and x=1.
−1=2⋅1−3
Check if the equation is a true statement.
−1=−1
Thi is a true statement.
⇒A lies on g.
B does not lie on any of the straight lines. This can be clearly seen in the sketch.
C is plugged into h: 5=−0,5⋅(−6)+3⇒5=3+3 This statement is false, so C does not lie on h.
D is plugged into h: 55=−0.5⋅(−102)+3⇒55=51+3 This statement is false, so D does not lie on h.
E is plugged into g: 87=2⋅45−3 This statement is true, so E lies on g.
Part 2
Completing coordinates
h:y=−0.5x+3 ; P(5∣?)
The given coordinate of the point (the x-coordinate) is inserted into the function equation and the missing y-coordinate is calculated from it.
y=−0.5⋅5+3=−2.5+3=0.5
⇒P(5∣0,5)
Q: y=−0.5⋅(−3.5)+3=1.75+3=4.75 ⇒ Q(−3.5∣4.75)
R: 12=−0.5x+3⇒0.5x=−9⇒x=−18 ⇒ R(−18∣12)
S: −7.5=−0.5x+3⇒0.5x=10.5⇒x=21 ⇒ S(21∣−7.5)
Part 3
Proof for T
T(2.4∣1.8)
Insert the coordinates of T into both line equations. If the statements are true, T lies on the lines.
on g: 1.8=2⋅2.4−3
1.8=4.8−3
1.8=1.8
on h: 1.8=−0.5⋅2.4+3
1.8=−1.2+3
1.8=1.8
⇒Both equations give correct statements, so the point T lies on both straight lines.
⇒T Is the intersection point of the lines.
- 5
Draw the graphs of the following lines including the point of intersection with the y-axis and a gradient triangle. Calculate the point of intersection with the x-axis and check the result using the graph.
f(x)=2x−5
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=2x−5
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−5)
⇒mf=2
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
2x−5 = 0 +5 2x = 5 :2 x0 = 2.5 ⇒Px(2.5∣0)
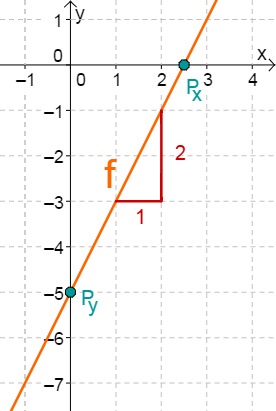
Do you have a question?
f(x)=−x−3
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=−x−3
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−3)
⇒mf=−1
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−x−3 = 0 +x −3 = x0 ⇒Px(−3∣0)
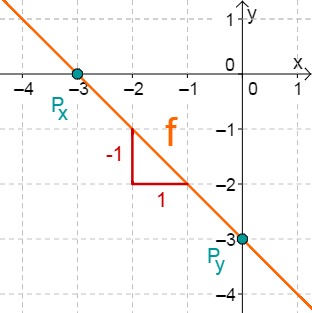
Do you have a question?
f(x)=21x+1
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=21x+1
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣1)
⇒mf=21
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
21x+1 = 0 −1 21x = −1 ⋅2 x0 = −2 ⇒Px(−2∣0)
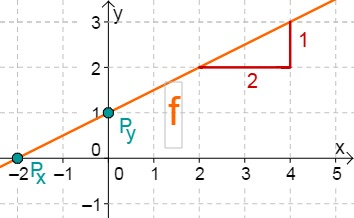
Do you have a question?
f(x)=−21x−2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=−21x−2
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−2)
⇒mf=−21
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−21x−2 = 0 +2 −21x = 2 ⋅(−2) x0 = −4 ⇒Px(−4∣0)
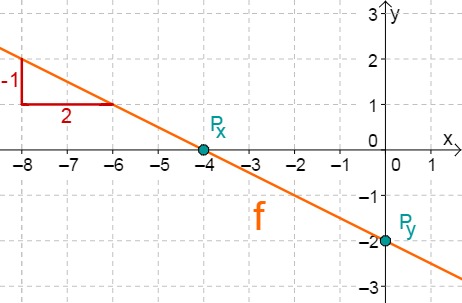
Do you have a question?
f(x)=31x−21
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=31x−21
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0−21)
⇒mf=31
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
31x−21 = 0 +21 31x = 21 ⋅3 x0 = 23 ⇒Px(23∣0)
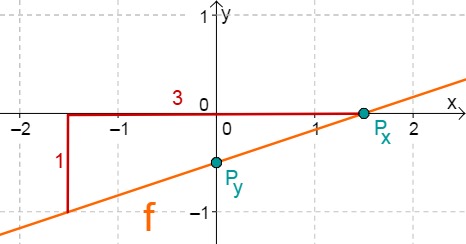
Do you have a question?
f(x)=−41x+23
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=−41x+23
First read off the y-axis intercept and the slope from the function equation.
⇒Py(023)
⇒mf=−41
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−41x+23 = 0 −23 −41x = −23 ⋅(−4) x0 = 6 ⇒Px(6∣0)
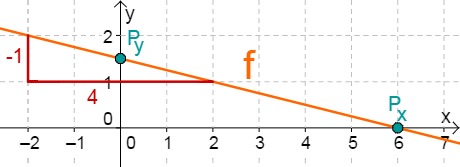
Do you have a question?
f(x)=32x+2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=32x+2
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣2)
⇒mf=32
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
32x+2 = 0 −2 32x = −2 :32 x0 = −3 ⇒Px(−3∣0)
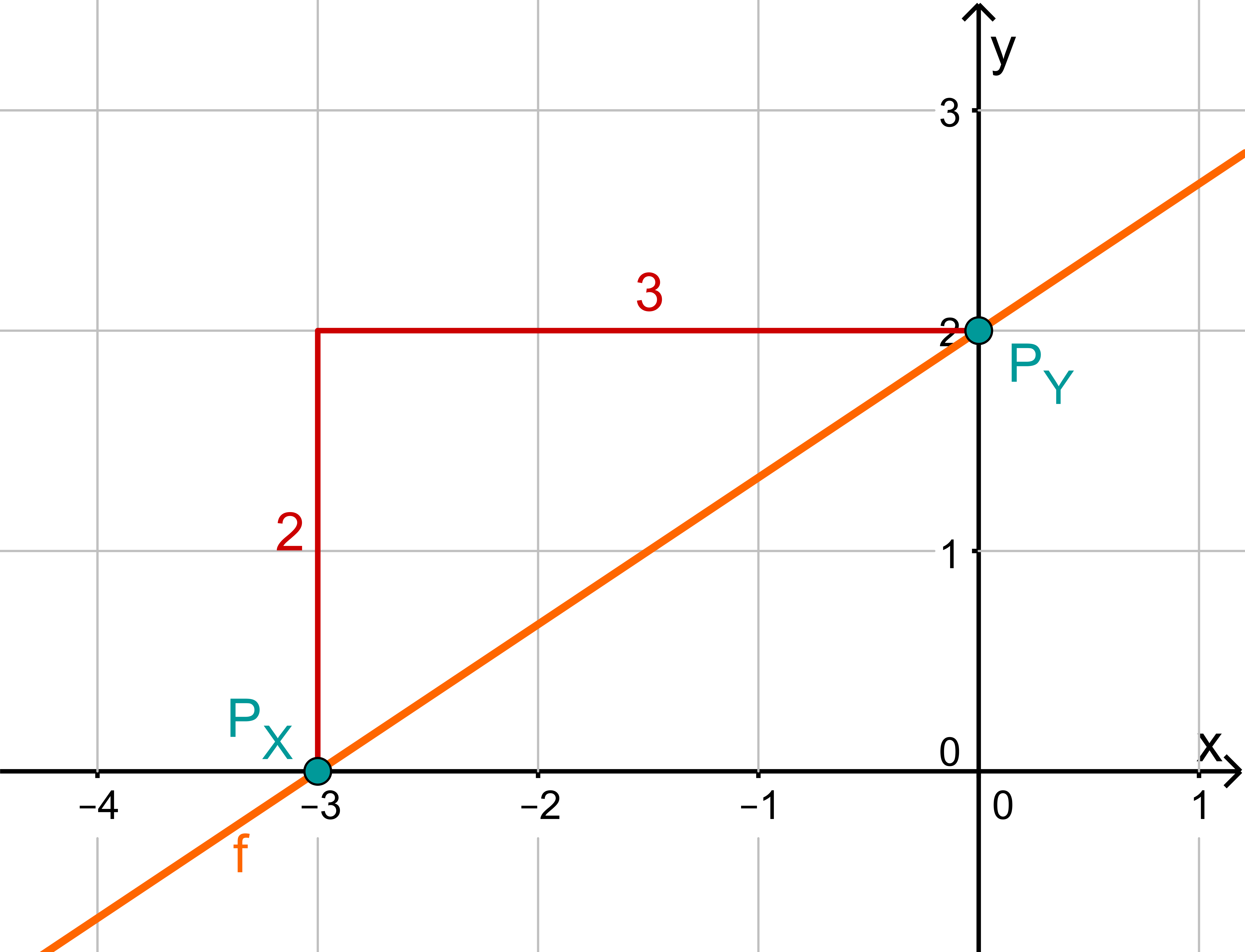
Do you have a question?
f(x)=−43x−1
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=−43x−1
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−1)
⇒mf=−43
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−43x−1 = 0 +1 −43x = 1 :(−43) x0 = −34 ⇒Px(−34∣0)
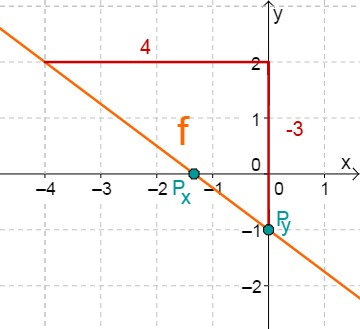
Do you have a question?
f(x)=−3x+105
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=−3x+105
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0105)
⇒mf=−3
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
−3x+105 = 0 −105 −3x = −21 :(−3) x0 = −61 ⇒Px(61∣0)
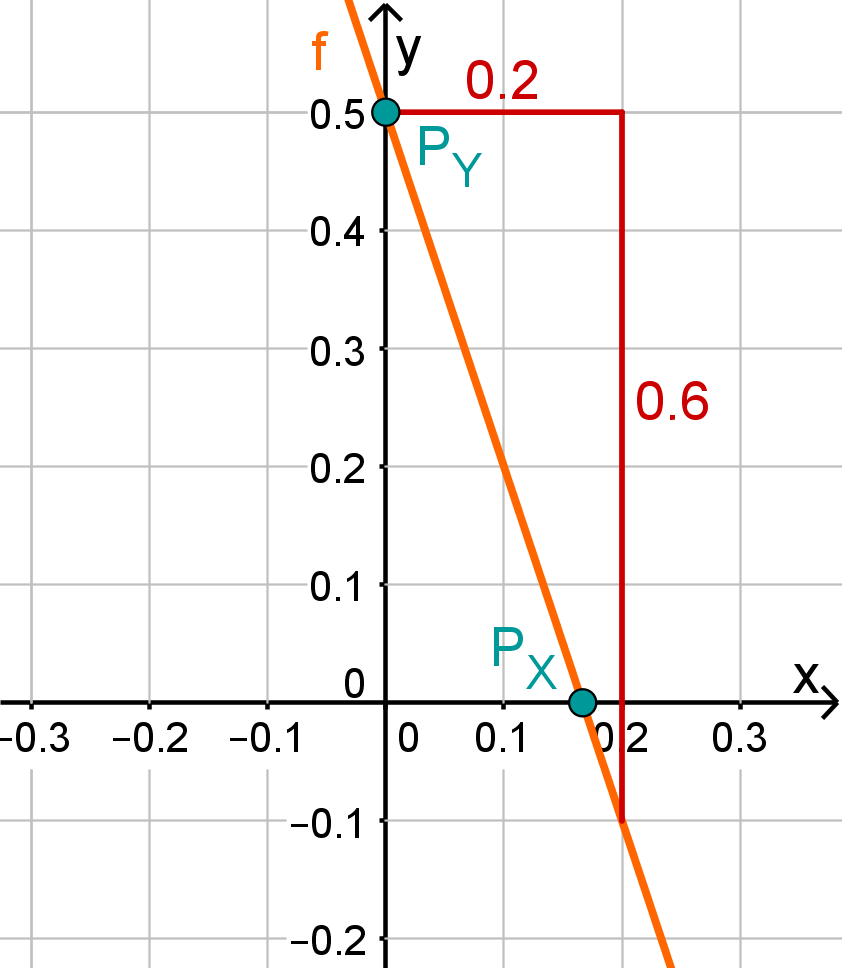
Do you have a question?
f(x)=75x−412
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lines in coordinate systems
f(x)=75x−412=75x−3
First read off the y-axis intercept and the slope from the function equation.
⇒Py(0∣−3)
⇒mf=75
Calculate the intersection point with the x-axis. This is done by setting the function term equal to 0.
75x−3 = 0 +3 75x = 3 :75 x0 = 521 ⇒Px(521∣0)
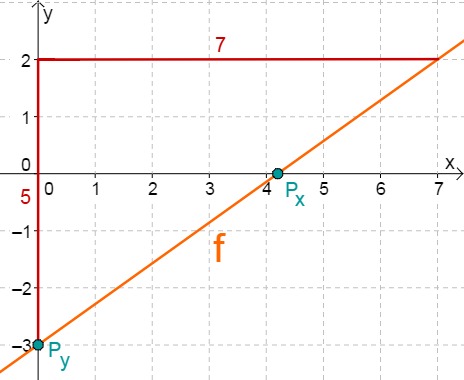
Do you have a question?
- 6
Draw the lines y=3x−2 and y=−43x+1 into a coordinate system. Determine the zeros and the point of intersection.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Draw the graphs
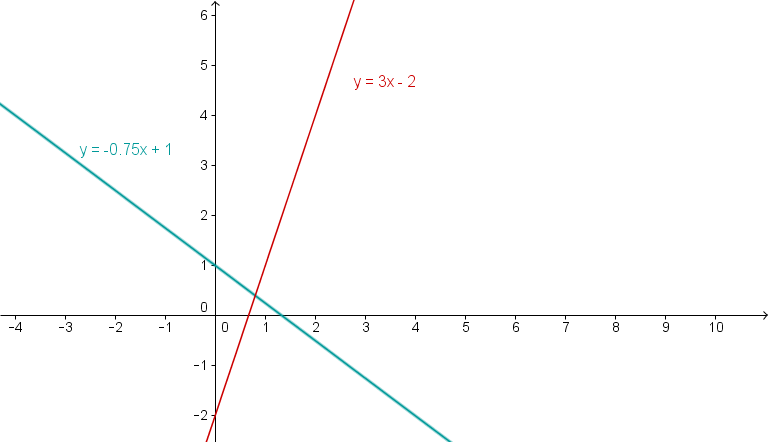
Determining the zeros
y=3x−2
Set y=0 to determine the zero point. This is the point where the line intersects the x-axis.
3x−2 = 0 +2 3x = 2 :3 xN1 = 32 Proceed in the same way for the second line.
y = −43x+1 ↓ Set y=0 to determine the zero.
−43x+1 = 0 −1 −43x = −1 :(−43) x = 431 ↓ You divide by a fraction -> multiply by the reciprocal value
xN2 = 34 Determining of the intersection point
Set the two function equations equal. The straight lines intersect where both have the same y-value at the same x-position.
3x−2 = −43x+1 +43x +2 3x+43x = 1+2 3.75x = 3 :3.75 x = 3.753 xS = 0.8 ↓ Plug xS into one of the two functions.
y = 3⋅0.8−2 y = 2.4−2 yS = 0.4 ⇒S(0,8∣0,4)
The intersection point is at S(0.8∣0.4).
- 7
Determine the intersection points with the coordinate axes of the following straight lines.
y=−2x+3.5
Intersection with the x-axis
Calculate the intersection of the line with the x-axis.
Set the expression for the line equation equal to 0 and solve for x.
02xx===−2x+3.53.51.75∣+2x∣:2
⇒ The line intersects the x-axis at Sx(1.75∣0).
Intersection with the y-axis
Calculate the intersection of the line with the y-axis.
To do this, plug the value x=0 into the expression for the straight line equation.
y=−2⋅0+3.5
y=3.5
⇒ The line intersects the y-axis at Sy(0∣3.5).
Do you have a question?
y=5x−7
Intersection with the x-axis
Calculate the intersection of the line with the x-axis.
Set the expression for the line equation equal to 0 and solve for x.
05xx===5x−7757=1.4∣+7∣:5
⇒ The line intersects the x-axis at Sx(1.4∣0).
Intersection with the y-axis
Calculate the intersection of the line with the y-axis.
To do this, plug the value x=0 into the expression for the straight line equation.
y=5⋅0−7
y=−7
⇒ The line intersects the y-axis at Sy(0∣−7).
Do you have a question?
y=23x+2
Intersection with the x-axis
Calculate the intersection of the line with the x-axis.
Set the expression for the line equation equal to 0 and solve for x.
023xx===23x+2−2−34∣−2∣⋅32
⇒ The line intersects the x-axis at Sx(−34−∣0).
Intersection with the y-axis
Calculate the intersection of the line with the y-axis.
To do this, plug the value x=0 into the expression for the straight line equation.
y=23⋅0+2
y=2
⇒ The line intersects the y-axis at Sy(0∣2).
Do you have a question?
y=−52x+25
Intersection with the x-axis
Calculate the intersection of the line with the x-axis.
Set the expression for the line equation equal to 0 and solve for x.
052xx===−52x+2525425=6.25∣+52x∣⋅25
⇒ The line intersects the x-axis at Sx(6.25∣0).
Intersection with the y-axis
Calculate the intersection of the line with the y-axis.
To do this, plug the value x=0 into the expression for the straight line equation.
y=−52⋅0+25
y=25=2.5
⇒ The line intersects the y-axis at Sy(0∣2.5).
Do you have a question?
y=2(x−32)
To obtain a general line equation y=m⋅x+t, multiply out the bracket
y=2(x−32)
y=2x−34
Intersection with the x-axis
Calculate the intersection of the line with the x-axis.
Set the expression for the line equation equal to 0 and solve for x.
02xx===2x−343432∣+34∣:2
⇒ The line intersects the x-axis at Sx(32∣0).
Intersection with the y-axis
Calculate the intersection of the line with the y-axis.
To do this, plug the value x=0 into the expression for the straight line equation.
y=2⋅0−34
y=−34
⇒ The line intersects the y-axis at Sy(0∣−34).
Do you have a question?
y=−34−21x
Transform the equation
To obtain a general line equation y=m⋅x+t, swap both elements on the right side.
y=−34−21x
y=−21x−34
Intersection with the x-axis
Calculate the intersection of the line with the x-axis.
Set the expression for the line equation equal to 0 and solve for x.
021xx===−34−21x−34−38=−232∣+21x∣⋅2
⇒ The line intersects the x-axis at Sx(−38∣0).
Intersection with the y-axis
Calculate the intersection of the line with the y-axis.
To do this, plug the value x=0 into the expression for the straight line equation.
y=−21⋅0−34
y=−34
⇒ The line intersects the y-axis at Sy(0∣−34).
Do you have a question?
- 8
Set up the function equation for the line through the points P(−25∣30) and Q(55∣−30) and calculate the intersection of the line with the x-axis.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
P(−25∣30); Q(55∣−30)
Determine the slope m of the general line equation using the difference quotient .
m=−25−5530−(−30)=−8060=−43
Insert m and the coordinates of a point, e.g. P(−25∣30), into the general line equation.
30=4−3(−25)+t
Simplify: 4−3(−25)=4−3(−25)=43⋅25=475
30 = 475+t −475 ↓ solve for t
t = 30−475 t = 445 ⇒y=−43x+445
Intersection with the x-axis
At the intersection with the x-axis the y-value is 0.
0=4−3x+445
Solve for x. To do this, we use ⋅3−4
Note that both summands must be multiplied.
0=4⋅3(−3)(−4)x+4⋅345(−4)
4⋅3(−3)(−4)=123⋅4=1212=1
0=x+12−180
0=x−15
Add 15
x=15
⇒ The line intersects the x-axis at S(15∣0).
- 9
Transform the equation into the form y=ax+b.
2x−y=6
x=21(y+1)
x = 21(y+1) ⋅2 ↓ The fraction on the right side vanishes because 21⋅2=1 .
2x = y+1 −1 ↓ Swap the left and right sides.
y = 2x−1 Do you have a question?
52y=2x−1
52y = 2x−1 ⋅25 ↓ Note: On the right-hand side, each element is multiplied by 25:
52⋅y⋅25=1010⋅y=1⋅y;2x⋅25=210x=5x;−1⋅25=−25
y = 5x−25 Do you have a question?
y=3(2x−1)
- 10
Two lines f(x) and g(x) intersect on the x-axis in x=4.
Determine possible function terms.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
There are several solutions to this problem. We are looking for two different linear functions that both pass through the point (4∣0).
A very simple example would be f(x)=0, i.e. the x-axis and g(x)=x−4.
f(x) obviously runs through (4∣0). For g(x) this can also be checked very easily: g(4)=4−4=0.
Other possible functions are:
y=−x+4 , y=2x−8 (generally y=ax−4a for any a).
Consider the point through which both lines must pass.
Determine two different functions that go through this point.
- 11
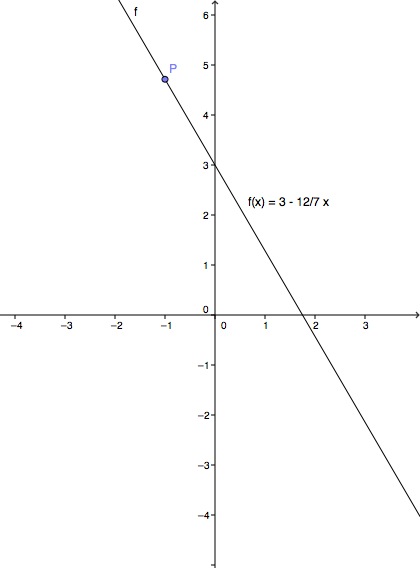
Consider the linear function f(x)=3−712x .
Draw the graph and mark the function value f(−1) .
Is the point P(7∣−1,54) on the graph of f(x)?
Check whether the point P(7∣−1.54) lies on the graph of the function.
To do this, insert the x-value 7 into the function equation y(x)=3−712x.
3−712⋅7 ≈ 3−712⋅2.65 ↓ multiply
≈ 3−4.543 ↓ subtract
≈ −1.543 Result
The point P(7∣−1.54) is not on the graph because the function value of 7 is a non-terminating decimal fraction and not the finite decimal fraction −1.54.
If you have calculated with rounded values, you might have mistakenly conclude that the point is on the graph. However, this is not the case.
Do you have a question?
- 12
Consider the lines g:y=2x−3 and h:y=−0.5x+3 .
Check whether the points A(1∣−1), B(0.5∣1.5), C(−6∣5), D(−102∣55) and E(45∣87) lie on one of the straight lines.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line equation
Checking with sketch
Select any point on the straight line, e.g. the y-axis sections (0∣−3) and (0∣3). Go from there 1 to the right and, corresponding to the slopes, mg=2 upwards or mh=−0.5 downwards. Connect the two points to form a straight line.

If you look at the course of the straight line and, for example, the position of point A, you will see that it will hardly lie on the straight line h, but probably on g. Similarly, you can decide for other points whether a mathematical check is worthwhile: Point D(−102/55) can only lie on h, for example.
Computational verification
Plug A(1∣−1) into g:
Plug the coordinates y=-1 and x=1 into the equation.
−1=2⋅1−3
That is a true statement.
⇒ A is on g.
B does not lie on any of the straight lines. This can be clearly seen in the sketch.
Plug C into h:
5=−0.5⋅(−6)+3
⇒ 5=3+3
This statement is false, so C is not on h.
Plug D into h:
55=−0.5⋅(−102)+3
⇒ 55=51+3
This statement is false, so D is not on h.
Plug E into g:
87=2⋅45−3
This statement is correct, so E lies on g.
Do you have a question?
Complete the coordinates so that the points lie on h: P(5∣?) , Q(−3,5∣?) , R(?∣12) , S(?∣−7,5).
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line equation
Complete coordinates
h:y=−0.5x+3 ; P(5∣?)
The given coordinate of the point (the x-coordinate) is inserted into the function equation and the missing y-coordinate is calculated from it.
y=−0.5⋅5+3=−2.5+3=0.5
⇒ P(5∣0,5)
Q: y=−0.5⋅(−3.5)+3=1.75+3=4.75 ⇒ Q(−3.5∣4.75)
R: 12=−0.5x+3⇒0.5x=−9⇒x=−18 ⇒ R(−18∣12)
S: −7.5=−0.5x+3⇒0.5x=10.5⇒x=21 ⇒ S(21∣−7.5)
Do you have a question?
Show that T(2.4∣1.8) lies on both straight lines. What does this mean?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Line equation
Proof for T
T(2.4∣1.8)
Plug the coordinates of T into both line equations. If the statements are true, T lies on the lines.
into g:
1.8 = 2⋅2.4−3 1.8 = 4.8−3 1.8 = 1.8 into h:
1.8 = −0.5⋅2.4+3 1.8 = −1.2+3 1.8 = 1.8 ⇒ Both equations give correct statements, so the point T lies on both lines.
⇒ T Is the intersection point of the lines.
Do you have a question?
This content is licensed under
CC BY-SA 4.0 → Info