Determining the equation of a function.
A line passes through the points P1 and P2 . Determine the equation of the function f(x), the points of intersection and draw the graph for the following values:
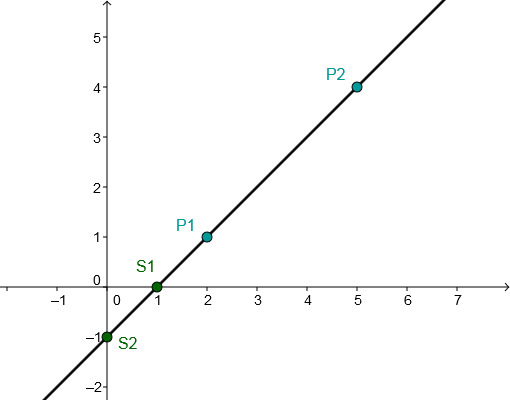
P1(2∣1)P2(5∣4)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Determining of the function equation
Substitute P1 and P2 into the general line equation . ⇒y=mx+t
Use the addition method.
1)1=m⋅2+t2)4=m⋅5+t
1)−2)−3 = −3m :(−3) m = 1 Plug m into 1).
1 = 1⋅2+t −2 t = −1 Setze t und m in die allgemeine Geradengleichung ein.
y=x−1⇒f(x)=x−1
Determining the axis intersection points
Set y=0 to determine the intersection with the x-axis.
x−1 = 1 +1 xN = 0 The intersection with the x-axis is S1(1∣0).
The point of intersection with the y-axis corresponds to the y-axis intercept t ⇒S2(0∣−1)
Drawing the graph
Connect either the two intersection points S1 and S2 or the two given points P1 and P2.
Or choose one of these points and go one to the right and one up according to the slope and connect these two points.
Do you have a question?
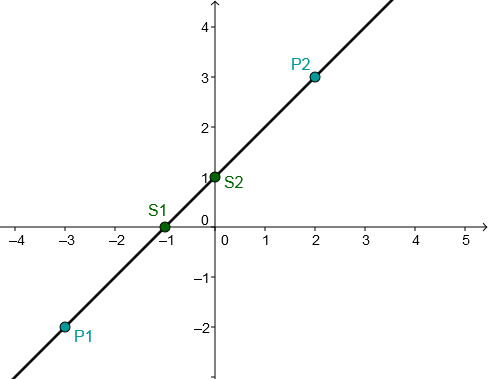
P1(−3∣−2)P2(2∣3)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Determining of the function equation
Substitute P1 and P2 into the general line equation . ⇒y=mx+t
Use the addition method.
1)−2=m⋅(−3)+t2)3=m⋅2+t
1)−2)−5 = −5m :(−5) m = 1 ↓ Plug m into 2).
3 = 2+t −2 t = 1 ↓ Plug m and t into the general line equation.
y = x+1⇒f(x)=x+1 Determining the axis intersection points
Set y=0 to determine the intersection with the x-axis.
x+1 = 0 −1 xN = −1 The intersection with the x-axis is S1(−1∣0).
The point of intersection with the y-axis corresponds to the y-axis intercept t ⇒S2(0∣−1) ⇒S(0∣1)
Drawing the graph
Connect either the two intersection points S1 and S2 or the two given points P1 and P2.
Or choose one of these points and go one to the right and one up according to the slope and connect these two points.
Do you have a question?
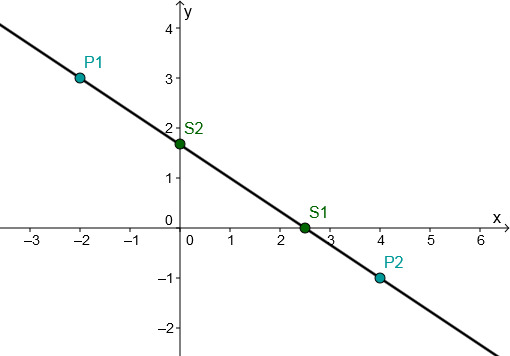
P1(−2∣3)P2(4∣−1)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Determining of the function equation
Substitute P1 and P2 into the general line equation . ⇒y=mx+t
Use the addition method.
1)3=−2m+t2)−1=4m+t
1)−2)4=−6m ∣:(−6)
Shorten the fractions. ⇒ m=−64
Plug m into 1). ⇒ m=−32
Multiply. ⇒ 3=−2(−32)+t
3=34+t −34
Subtract. ⇒ t=3−34
Setze m und t in die allgemeine Geradengleichung ein. ⇒ t=132
y=−32x+132
Determining the axis intersection points
Set y=0 to determine the intersection with the x-axis.
−32x+132=0 −132
−32x=−132=−35 :(−32)
Divide the fractions ⇒ x=−32−35
xN=−35⋅(−23)=25=2.5
The intersection with the x-axis is S1(25∣0)
The point of intersection with the y-axis corresponds to the y-axis intercept t ⇒S2(0∣−1) ⇒S(0∣35)
Drawing the graph
Connect either the two intersection points S1 and S2 or the two given points P1 and P2.
Or choose one of these points and go 3 to the right and 2 down according to the slope and connect these two points.
Do you have a question?
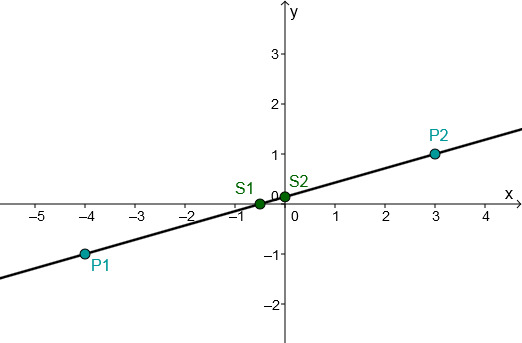
P1(−4∣−1)P2(3∣1)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Determining of the function equation
Substitute P1 and P2 into the general line equation . ⇒y=mx+t
Use the addition method. ⇒ 1)−1=−4m+t2)1=3m+t
1)−2)−2=−7m ∣:(−7)
Plug m into 2). ⇒ m=72
1=72⋅3+t −76
Subtract. ⇒ t=1−76
Plug m and t into the general line equation. ⇒t=71
y=72x+71⇒f(x)=72x+71
Determining the axis intersection points
Set y=0 to determine the intersection with the x-axis.
72x+71=0 −71
72x=−71 :(72)
Divide the fractions. → Multiply by the inverse. ⇒x=72−71
Multiply. ⇒ x=−71⋅27
xN=−21
The intersection with the x-axis is S1(−21∣0).
The point of intersection with the y-axis corresponds to the y-axis intercept t ⇒S2(0∣−1) ⇒S2(0∣71)
Drawing the graph
Connect either the two intersection points S1 and S2 or the two given points P1 and P2.
Or choose one of these points and go 7 to the right and 2 up according to the slope and connect these two points.
Do you have a question?
P1(−3∣29)P2(4∣−1)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Determining of the function equation
Substitute P1 and P2 into the general line equation . ⇒y=mx+t
Use the addition method. ⇒1)29=−3m+t2)−1=4m+t
1)−2)211=−7m ∣:(−7)
Plug m into 2) . ⇒m=−7211=−1411
Multiply. ⇒−1=−1411⋅4+t
−1=−1444+t +1444
Plug m and t into the general equation of a straight line. ⇒t=1430
y=−1411x+1430
Determining the axis intersection points
Set y=0 to determine the intersection with the x-axis.
−1411x+1430=0 −1430
−1411x=−1430 :(−1411) Divide the fractions. That means, multiply by the inverse.
Multiply. ⇒x=−1430⋅(−1114)
xN=1130
The intersection with the x-axis is S1(1130∣0)
The point of intersection with the y-axis corresponds to the y-axis intercept t ⇒S2(0∣−1) ⇒S(0∣1430)
Drawing the graph
Connect either the two intersection points S1 and S2 or the two given points P1 and P2.
Or choose one of these points and go 14 to the right and 11 down according to the slope and connect these two points.
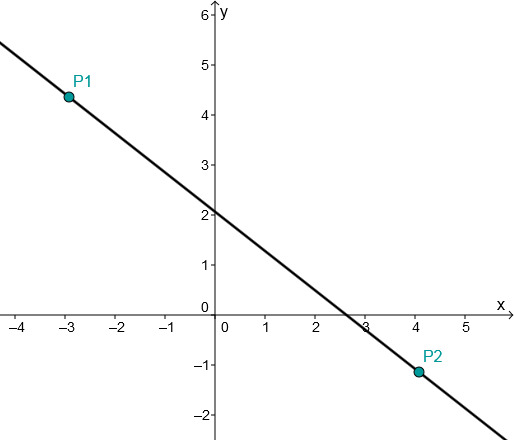
Do you have a question?
P1(−4∣−2)P2(27∣4)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Determining of the function equation
Substitute P1 and P2 into the general line equation . ⇒y=mx+t
Use the addition method. ⇒1)−2=−4m+t2)4=3.5m+t
−6=−7.5m ∣:(−7.5)
Divide. ⇒m=−7.5−6
Plug m into 1). ⇒m=0.8
Multiply. ⇒−2=0.8⋅(−4)+t
−2=−3.2+t ∣+3.2
Plug m and t into the general equation of a straight line. ⇒t=1.2
y=0.8x+1.2⇒f(x)=0.8x+1.2
Determining the axis intersection points
Set y=0 to determine the intersection with the x-axis.
0.8x+1.2=0 ∣−1.2
0.8x=−1.2 ∣:0.8
Dividiere. ⇒x=0.8−1.2
xN=−1.5
The intersection with the x-axis is S1(−1.5∣0)
The point of intersection with the y-axis corresponds to the y-axis intercept t ⇒S2(0∣−1) ⇒S(0∣1.2)
Drawing the graph
Connect either the two intersection points S1 and S2 or the two given points P1 and P2.
Or choose one of these points and go 1 to the right and 0.8 up according to the slope and connect these two points.

Do you have a question?
This content is licensed under
CC BY-SA 4.0 → Info
