Skip to content or footer
SerloThe Open Learning Platform

Relations between trigonometric functions

Sine, cosine and tangent are in different relationships. A distinction is made between the complement relationships and the supplement relationships.

Complement relationships

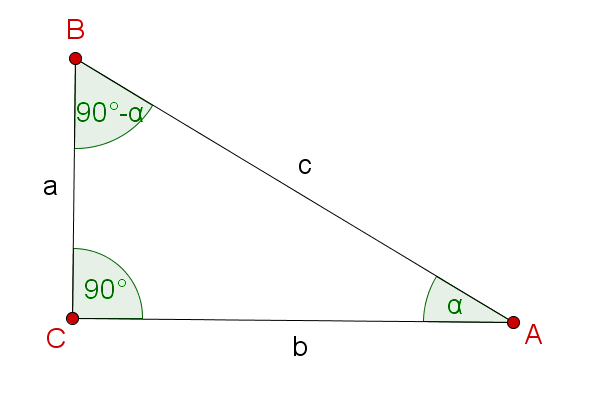
Dreieck

  • sin⁡(90∘−α)=cos⁡(α)\sin(90^{\circ}-\alpha)=\cos(\alpha)

  • cos⁡(90∘−α)=sin⁡(α)\cos(90^\circ-\alpha)=\sin(\alpha)

  • tan⁡(90∘−α)=1tan⁡(α)\tan(90^\circ-\alpha)=\frac1{\tan(\alpha)}

Since in a triangle the sum of the interior angles is always 180°180°, the following applies in a right triangle β=90°−α\beta=90°-\alpha.

Using the sine, cosine and tangent formulas, you can see:

sin⁡(90°−α)=opposite cathetushypotenuse=bc\sin(90°-\alpha)=\frac{\text{opposite cathetus}}{\text{hypotenuse}}=\frac{b}{c}

cos⁡(α)=adjacent cathetushypotenuse=bc.\cos(\alpha)=\frac{\text{adjacent cathetus}}{\text{hypotenuse}}=\frac{b}{c}.

Hence,  sin⁡(90°−α)=cos⁡(α)\;\sin(90°-\alpha)=\cos(\alpha).

The other equations can be explained in the same way.

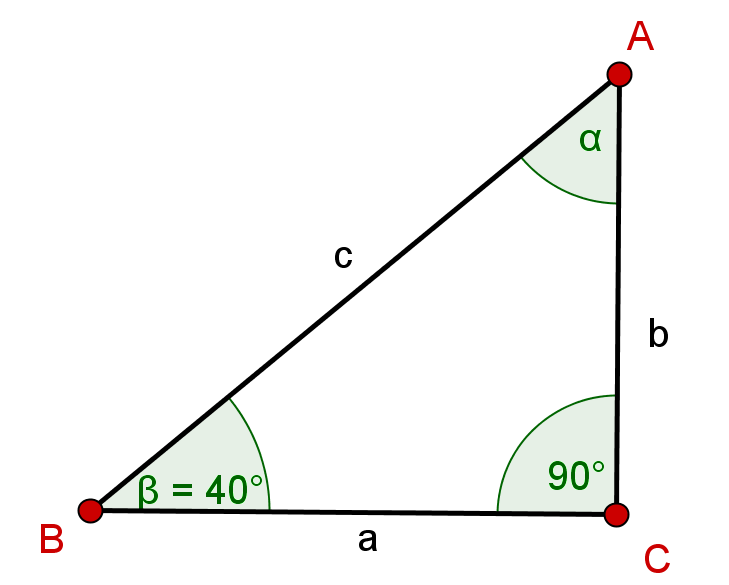
Example

Consider the given triangle. Calculate cos⁡(α) \cos(\alpha) in the same way as above.

Dreieck

With the complement relation you can equate cos⁡(α) \cos(\alpha) and sin⁡(90°−α) \sin(90°-\alpha).

cos⁡(α)=sin⁡(90°−α)\cos(\alpha)=\sin(90°-\alpha)

Because of the sum of the interior angles, the following equation applies.

sin⁡(90°−α)=sin⁡(β)\sin(90°-\alpha)=\sin(\beta)

Insert the value of β\beta, calculate the result and round it to 22 decimal places.

sin⁡(β)=sin⁡(40°)≈0.59.\sin(\beta)=\sin(40°)\approx0.59.

Therefore, cos⁡(α)≈0.59.\cos(\alpha)\approx0.59.

Supplement relationships

Sine

Kosine

Tangent

sin⁡(180°+α)=−sin⁡(α)\sin(180° + \alpha)=-\sin(\alpha)

cos⁡(180∘+α)=−cos⁡(α)\cos(180^\circ+\alpha)=-\cos(\alpha)

tan⁡(180∘+α)=+tan⁡(α)\tan(180^\circ+\alpha)=+{\textstyle\tan}(\alpha)

sin⁡(180°−α)=+sin⁡(α)\sin(180°-\alpha)=+\sin(\alpha)

cos⁡(180°−α)=−cos⁡(α)\cos(180°-\alpha)=-\cos(\alpha)

tan⁡(180∘−α)=−tan⁡(α)\tan(180^\circ-\alpha)=-\tan(\alpha)

sin⁡(360∘−α)=−sin⁡(α)\sin(360^\circ-\alpha)=-\sin(\alpha)

cos⁡(360∘−α)=+cos⁡(α)\cos(360^\circ-\alpha)=+\cos(\alpha)

tan⁡(360∘−α)=−tan⁡(α)\tan(360^\circ-\alpha)=-\tan(\alpha)

Visualization

sin⁡(180°+α)=−sin⁡(α)  \sin(180°+\alpha)=-\sin(\alpha)\; and   cos⁡(180°+α)=−cos⁡(α)  \;\cos(180°+\alpha)=-\cos(\alpha)\; can be tested, here


This content is licensed under
CC BY-SA 4.0 → Info