The sine, cosine and tangent functions are the most important trigonometric functions.
Sine, cosine and tangent describe the ratio of side lengths in a right triangle depending on one of the acute angles. They are defined as follows.
The "adjacent cathetus" is the cathetus that encloses the angle together with the hypotenuse. The "opposite cathetus" is the cathetus opposite to the angle (see figure).

Here in the picture, the "adjacent cathetus" is marked with a , the "opposite cathetus" with an and the hypotenuse with a .
Note: Side is opposite angle , is opposite and is opposite . Where is the right angle in this example.

The following relationships result from this:
Important function values
The following table of values shows the function values of the cosine, sine and tangent:
| |||||
- |
Attention: In the case we cannot form a triangle, because is not defined.
Dependencies
If you are given a right triangle, one side and one angle, you can use the trigonometric functions to calculate the remaining side lengths.
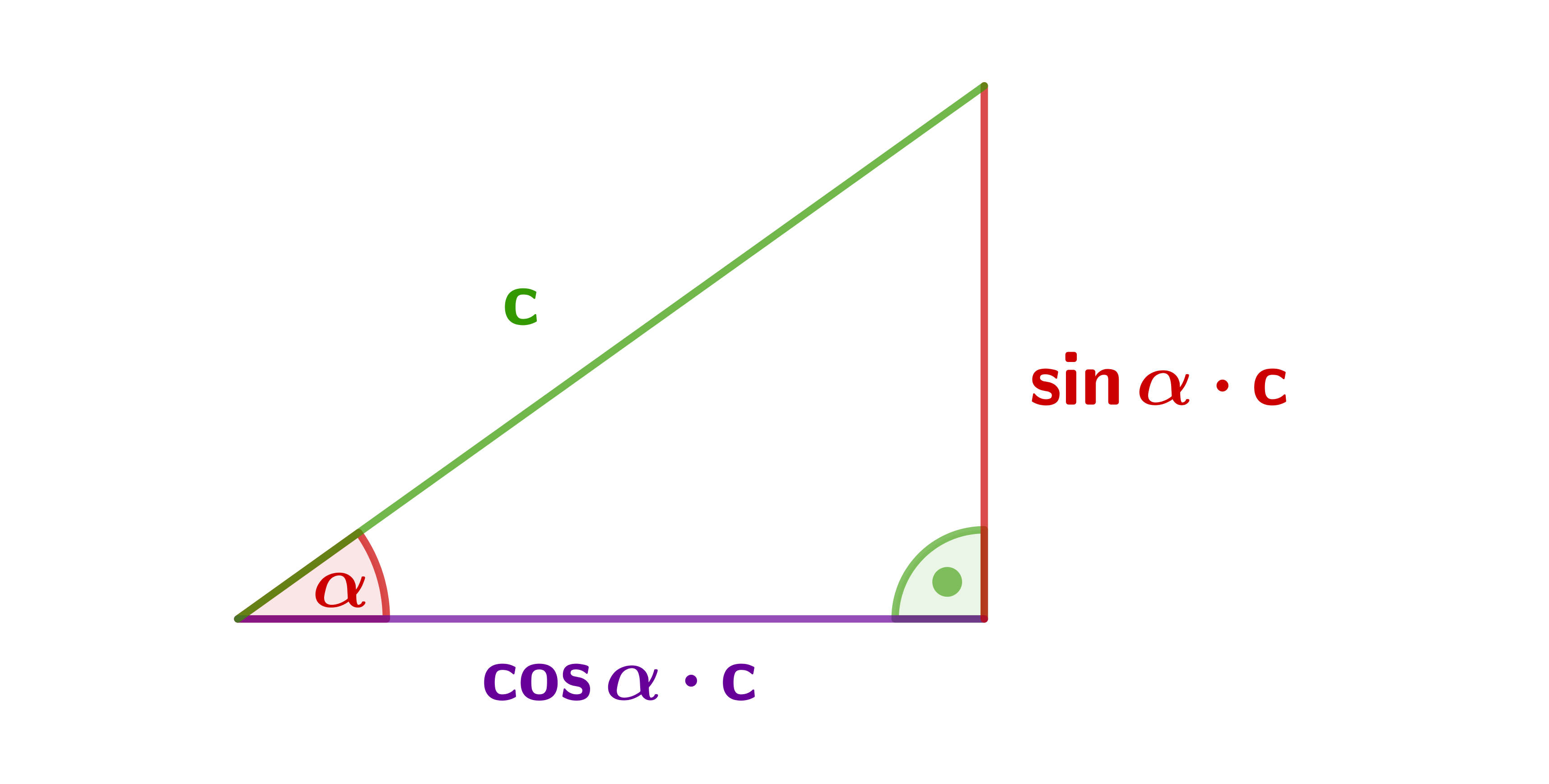
Hypotenuse is given.
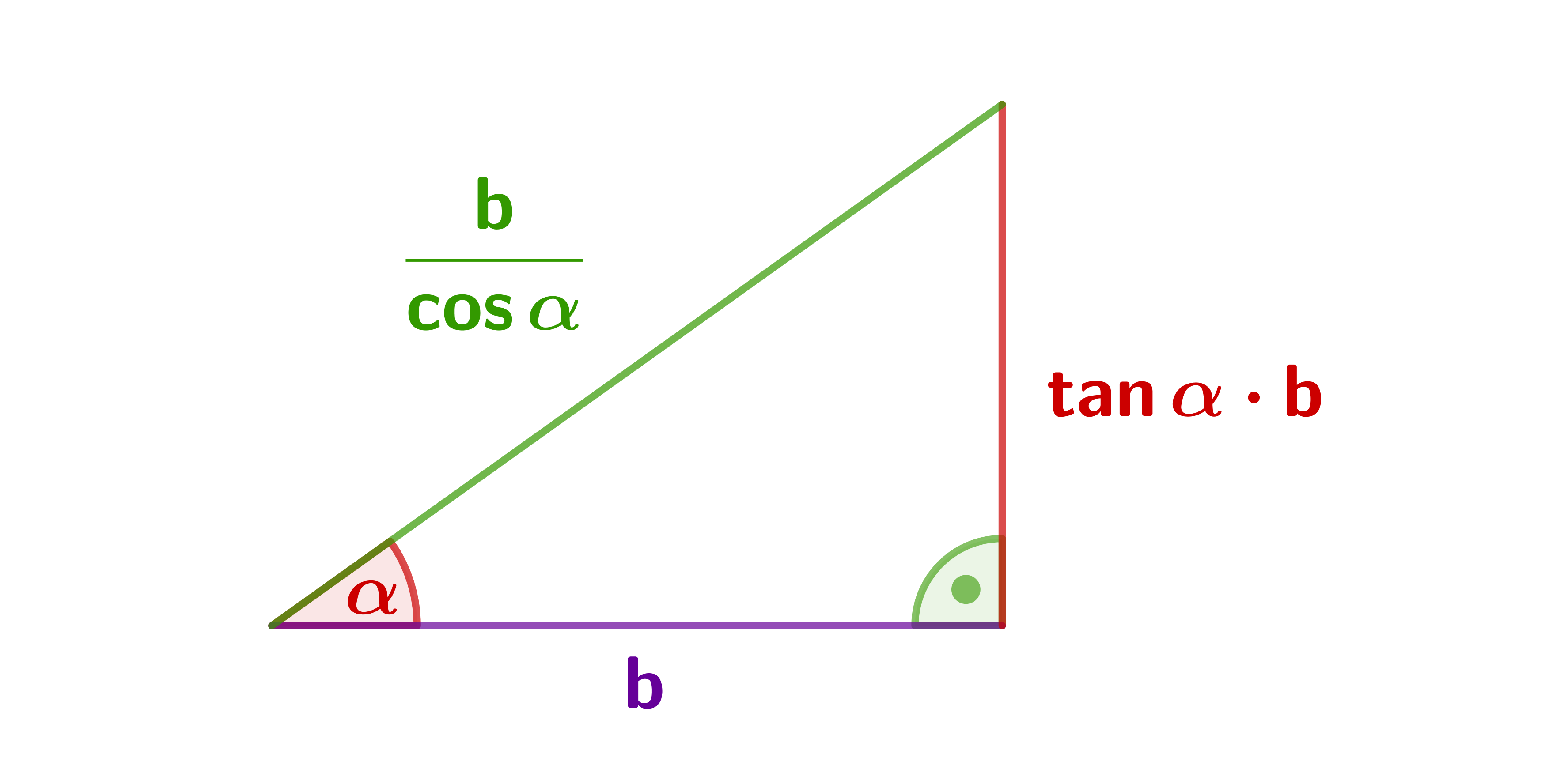
Adjacent cathetus is given.
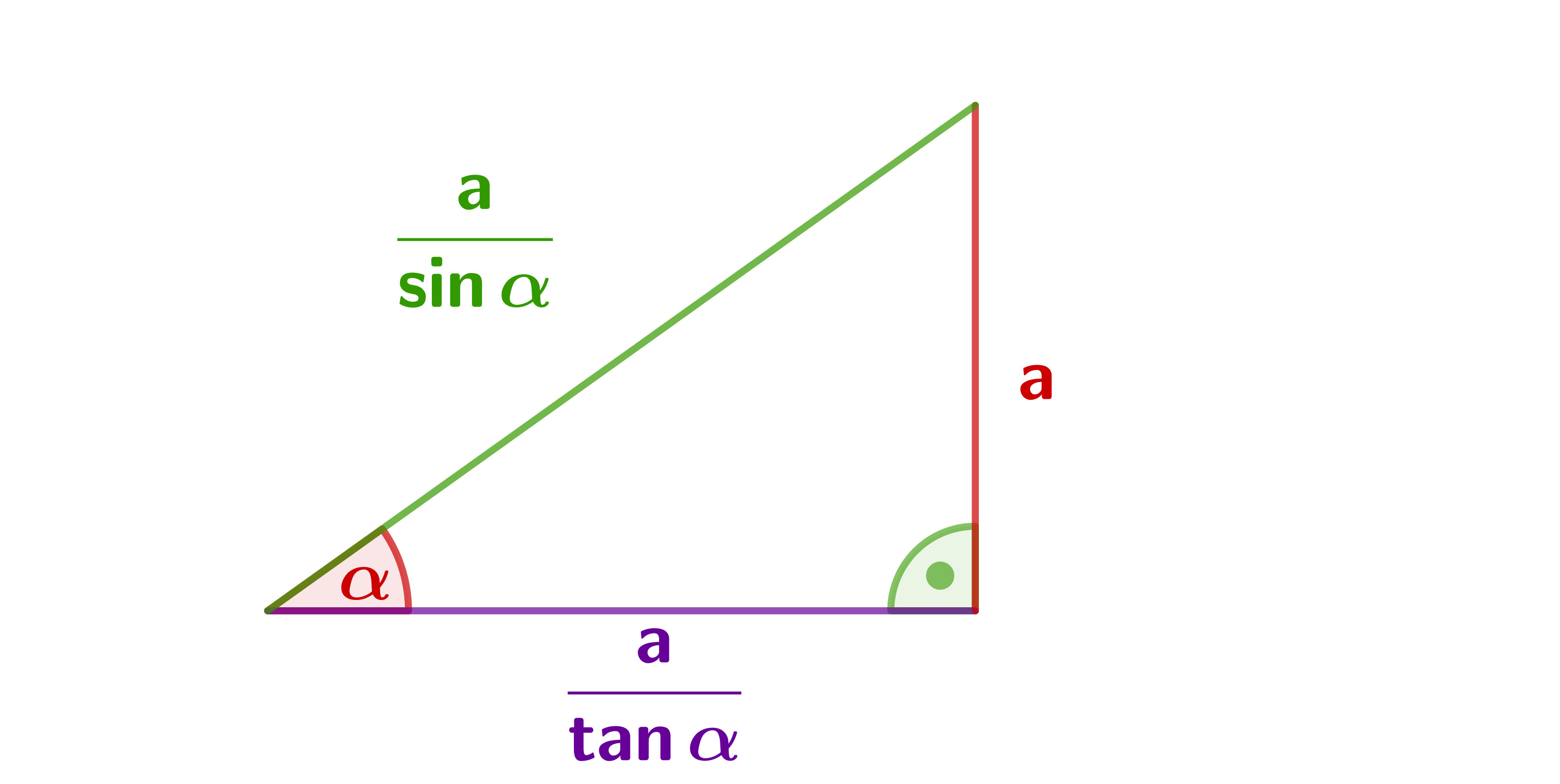
Opposite cathetus is given.
You obtain these formulas by resolving the definitions of sine, cosine and tangent for , and respectively.
In the first case, if the hypotenuse is given, it works as follows.
The other cases work in the same way.
Example
For a right triangle at , the length of the hypotenuse and the angle are given(first diagram).
Then the lengths of the adjacent side and the opposite side can be calculated using the sine and the cosine:
Calculation rules
There are some calculation rules for sine, cosine and tangent. Here, you learn about
writing the tangent as quotient of sine and cosine,
the trigonometric Pythagoras,
the addiotion theorems.
Tangent as quotient of sine and cosine
Directly via the definition from above, one obtains the following alternative representation for the tangent:
You can also simply recalculate the correctness of this equation:
Trigonometric Pythagoras
From the definition on the unit circle it follows directly from the Pythagorean theorem:
You can find a detailed explanation in the video below.
Addition theorems
The addition theorems make it possible to calculate the sine and cosine of a sum:
Further relationships between sine, cosine and tangent
In the article relations between trigonometric functions you can find more relationships of the functions.
Trigonometry on the unit circle
You can also use the unit circle to illustrate the angle relationships shown in the article. You can read more about this topic here: Trigonometry on the unit circle.
Sine, cosine and tangent function
You can also represent sine, cosine and tangent as functions. You can find out more about this in the article sine function and cosine function or tangent function.
Exercises: Sine, Cosine and Tangent
You can find more exercises in the following folder::
Exercises: Sine, Cosine and Tangent on a right triangle
