Consider the following graphs of linear functions:
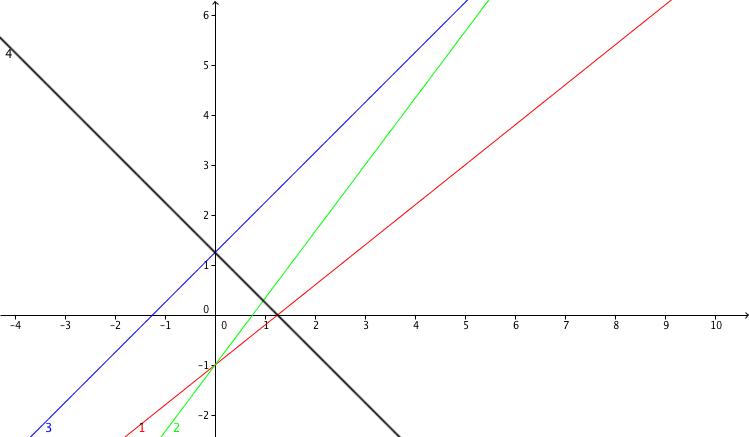
Which of the four graphs belongs to the equation y=45x−1 ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen linearer Funktionen zuordnen
Finde den Funktionsgraphen, der zur Funktionsgleichung y=45x−1 gehört.
Bestimme daher zunächst den y-Achsenabschnitt.
y(0)=45⋅0−1
Multipliziere und subtrahiere.
45⋅0−1=−1
Gebe den y-Achsenabschnitt an.
Der y-Achsenabschnitt ist -1, der Graph schneidet also im Punkt (0,-1) die y-Achse. Somit können nur Graph 1 (rot) und Graph 2 (grün) zu der Funktion gehören.
Betrachte nun die Steigung der Graphen. Gib zuerst die Funktionsgleichung der Funktion an.
y=45x−1
Gib die Steigung der Funktion an, indem du sie von der Geradengleichung abliest.
m=45
Graph 1 (rot)
Bestimme die Steigung von Graph 1 (rot), indem du ein Steigungsdreieck konstruierst. Lies dazu den Wert an der Stelle x2=1 ab.
x2=1
y2=y(x2)=−0.25
Für die Konstruktion eines Steigungsdreieck benötigst du einen zweiten Punkt. Gib dazu den schon berechneten Punkt des y-Achsenabschnitts an.
x1=0
y1=−1
Berechne nun die Steigung gemäß m=x2−x1y2−y1.
m=1−0−0.25−(−1)=10.75=0.75
Die Steigung des Graphen ist offenbar zu klein, als dass Graph 1 (rot) der zugehörige Funktionsgraph sein könnte.
Graph 2 (grün)
Bestimme die Steigung von Graph 2 (grün), indem du ein Steigungsdreieck konstruierst. Lies dazu den Wert an der Stelle x2=1 ab.
x2=1
y2=y(x2)=0.25
Gib den Punkt des y-Achsenabschnitts an.
x1=0
y1=−1
Für die Konstruktion eines Steigungsdreieck benötigst du einen zweiten Punkt. Gib dazu den schon berechneten Punkt des y-Achsenabschnitts an.
m=1−00.25−(−1)=11.25=1.25=45
Ergebnis
Der zugehörige Graph ist Graph 2 (grün), da seine Steigung und sein y-Achsenabschnitt mit der Geradengleichung übereinstimmen.
Do you have a question?
Determine (approximately) the function term to the graph 3.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
You have to find the general form of a line equation:
The general equation of a straight line is y=mx+t.
y-axis intercept
Determine the y-axis intercept of the function graph 3 (blue).
The y-axis intercept is the function value at the intersection of the function graph with the y-axis, i.e. the function value f(x) at x=0.
Read off the point where the function graph intersects the y-axis.
(x,∣f(x))=(0∣1.25)
Wrote down the y-axis intercept t.
t=1.25
Slope
Determine the slope/gradient of the function graph 3 (blue) using a gradient triangle and give the expression for the slope.
m=x2−x1y2−y1
Read off two points on graph 3 (blue) and then calculate the slope.
x1=0
y1=y(x1)=1.25
x2=−1
y2=y(x2)=0.25
Now calculate the slope m.
m=−1−00.25−1.25=−1−1=1
Result
The line equation of the function graph 3 (blue) is y(x)=x+1.25 .
Do you have a question?
This content is licensed under
CC BY-SA 4.0 → Info
