Further exercises: Linear functions
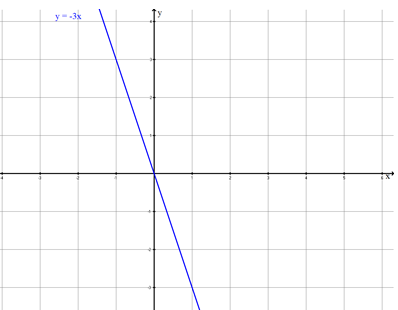
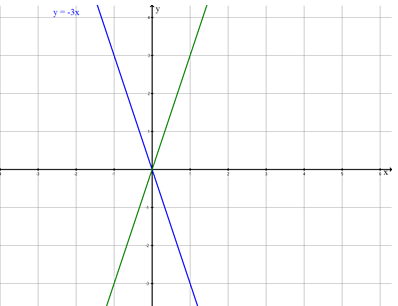
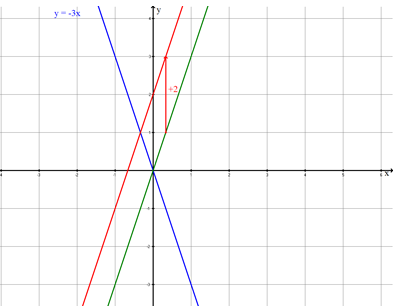
- 1
The straight line is mirrored on the -axis.
The mirrored straight line is then shifted upwards by 2 units.
Determine the equation of the new straight line;
a) by a drawing
b) by computation
- 2
Consider the functions and .
The straight line is to be shifted in the -direction so that and the shifted line intersect the -axis at the same point.
Determine the function term for the shifted line.
- 3
Consider the point with
Choose some values for and plot the corresponding points in a coordinate system.
How are the points located in the coordinate system? For which - values is the -coordinate equal to the -coordinate of point ?
- 4
Show that the line through and has the slope and intersects the y-axis at
- 5
Show that the points lie on a straight line for all .
Determine the equation of the straight line.
- 6
Find the function term of the linear function for:
- 7
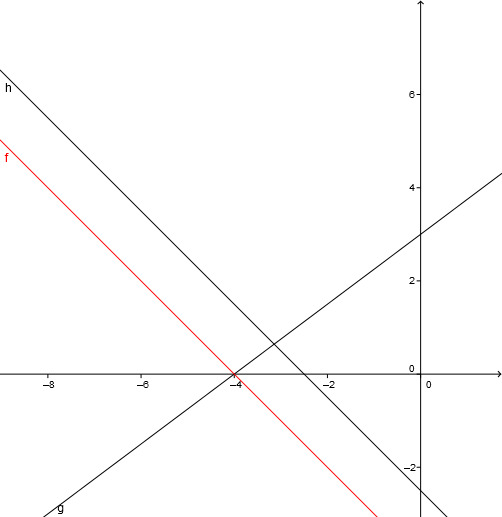
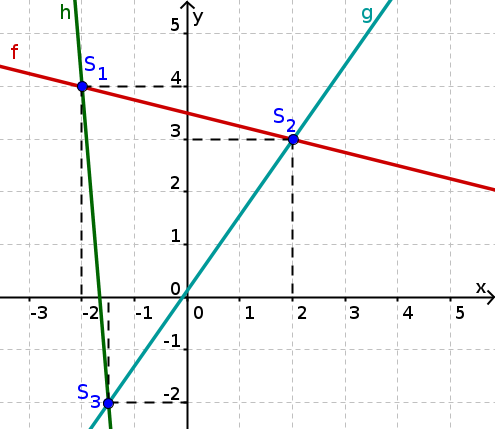
Determining intersection points
Three lines are drawn in the coordinate system. Read off the points of intersection from the figure.
- 8
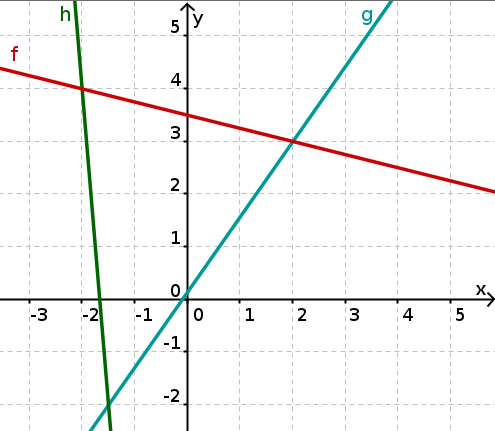
Determining intersection points
Consider a line and a line .
Determine the line equations of and .
Lies den Schnittpunkt ab.