Applied exercises: Linear functions

1
Are the following relations are linear, proportional or non-linear?
1. number of bought cucumbers $\mapsto$ total price of those cucumbers
  (assumed that there is no discount)
  linear
  proportional
  non-linear
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  The relation is linear and even proportional.
  The price of cucumbers is calculated per piece. Therefore, twice as many cucumbers cost twice as much and five times as many cucumbers cost five times as much.
  Example
  The graph of the price depending on the cucumber nurmber could look as follows:
  Do you have a question?
  Write it here 👉
2. age $\mapsto$ body height
  linear
  proportional
  non-linear
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  This relation is not linear, i.e. in particular not proportional.
  Until the age of about 18, people are still growing. After that, growth stops. Therefore, the relation cannot be linear.
  Example
  This is what the body height of a person over a lifespan may look like:
  (The graph is simplified)
  Do you have a question?
  Write it here 👉
3. amount of rice $\mapsto$ weight of a bowl with that rice in it
  linear
  proportional
  non-linear
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  This relation is linear, but not proportional.
  The weight of the filled bowl increases linearly with the amount of rice. However, since the bowl has its own weight, the relation is not proportional. The filled bowl does not weigh twice as much with double the amount of rice.
  Example
  For a bowl of $200 g$ , the weight function may look as follows:
  Do you have a question?
  Write it here 👉
4. value in € $\mapsto$ value in $
  linear
  proportional
  non-linear
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  The relation is linear and even proportional.
  The exchange rate between € and $ indicates how much $ you get for 1 €. The more monetary value you have in €, the higher its monetary value in $. Twice as much value in € means twice as much value in $. Ten times as much value in € means ten times as much value in $, etc. The relation is therefore linear and even proportional.
  Example
  This is what a money conversion function may look like:
  Do you have a question?
  Write it here 👉
5. study time for an exam $\mapsto$ score in the exam
  linear
  proportional
  non-linear
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  This relation is not linear, so in particular also not proportional.
  The more you study, the more likely it is that you will get a better grade and more points in the exam. However, after a certain period of study, you may have learned so well that you get (almost) full score in the exam. Further learning will then not lead to (much) further improvement.
  Example
  The graph of an associated function could look like this:
  Do you have a question?
  Write it here 👉
6. side length of a square $\mapsto$ area of the square
  linear
  proportional
  non-linear
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  This relation is not linear, so in particular also not proportional.
  The area of a square with side length a is calculated via $A_{\square}=a^2$ . Doubling the side length leads to a quadrupling of the area. A tripling of the side length leads to a ninefold increase in the area.
  You can also use further examples, as in the table of values below.
  The relation is thus not linear and not proportional.
  Example
  For example, take a square with a side length of 1 LU (length unit), 2LU, etc.. Then calculate the area of the square in AU (area units).
  a
  1 LU
  2 LU
  3 LU
  4 LU
  5 LU
  $A_\square$
  1 AU
  4 AU
  9 AU
  16 AU
  25 AU
  The graph of an associated function could look like this:
  Do you have a question?
  Write it here 👉
7. number of chocolate bars $\mapsto$ number of calories gained by the chocolate bars
  linear
  proportional
  non-linear
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  The relation is linear and even proportional.
  Each chocolate bar has a certain number of calories. If you eat twice as many chocolate bars, you eat twice as many calories as if you eat one chocolate bar. Three bars triple the calories, etc.
  Example
  The graph of an associated function could look like this:
  Do you have a question?
  Write it here 👉
8. number of drinks during a club visit $\mapsto$ total costs of the club visit
  (All drinks cost the same.)
  linear
  proportional
  non-linear
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  This relation is linear, but not proportional.
  You have to pay an entrance fee to get into a club. In addition, you pay a certain amount for each drink. Therefore, the costs have to be calculated as follows:
  $\text{cost}=\text{entrance fee}+\text{number of drinks}\cdot\text{price per drink}$
  Due to the entrance fee, the relation is not proportional.
  Example
  The graph of an associated function could look like this:
  Do you have a question?
  Write it here 👉
2
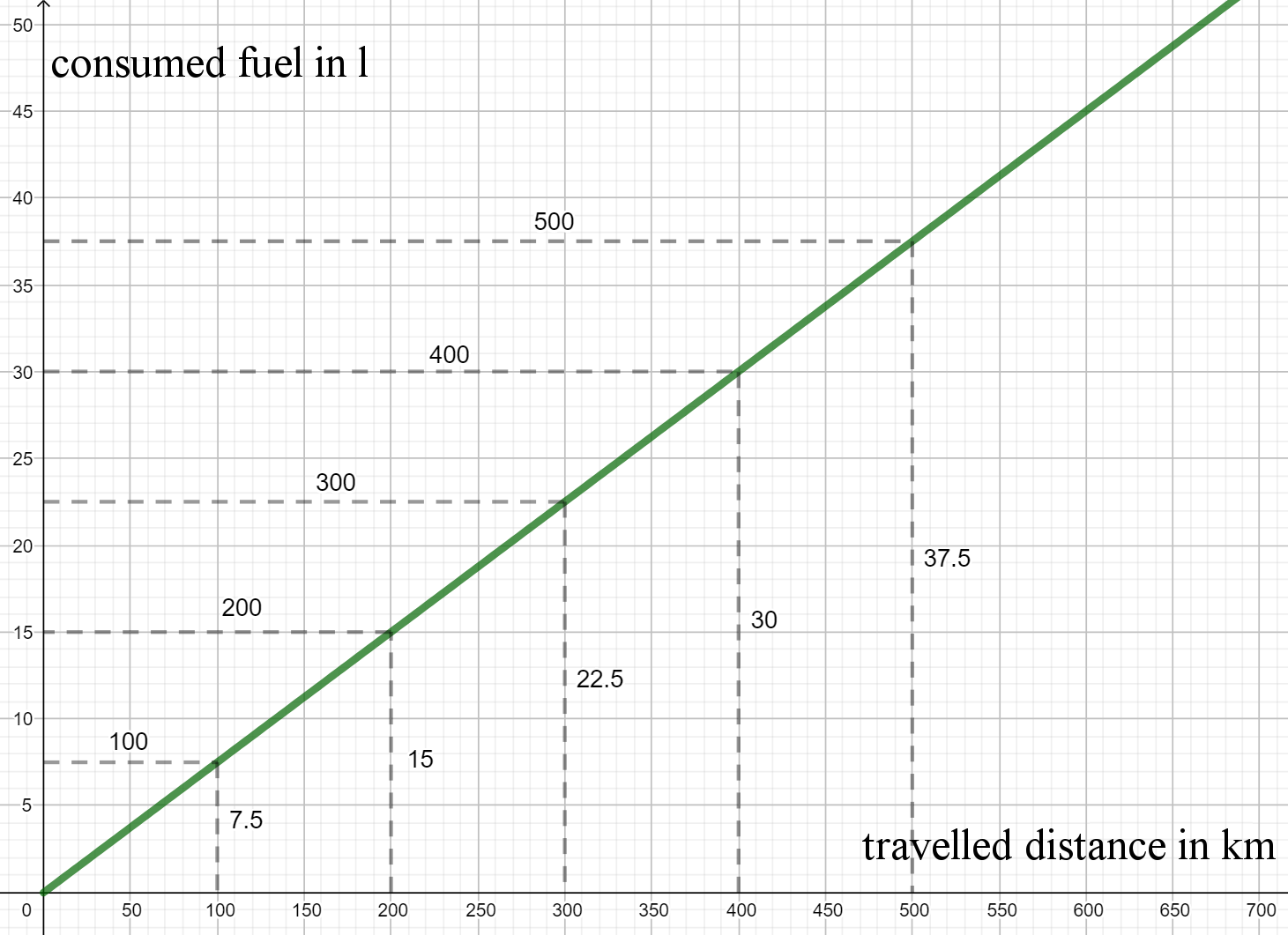
A car has a fuel supply of 56 liters of gasoline. It consumes 7.5 liters per 100 km.
1. Create a table for the consumption in liters for distances between 0km and 600km (with 100km between two values).
  
  distance traveled
  0 km
  100 km
  200 km
  300 km
  400 km
  500 km
  600 km
  fuel consumption
  0 l
  7.5 l
  15 l
  22.5 l
  30 l
  37.5 l
  45 l
  Do you have a question?
  Write it here 👉
2. Visualize the relation graphically.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  You can draw the function in your coordinate system by entering the points from the table in part a) and then connecting them by a line.
  Do you have a question?
  Write it here 👉
3. After how many km would the car run out of gasoline? In order to not run out of gasoline, one should refuel it if the supply has reached a level of 5L. After how many km will this point be reached?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  First, you should represent the gasoline consumption by a linear function. It has the form $f(x)\ =\ mx\ +\ b$ where $x$ stands for the travelled distance and f(x) for the consumed gasoline. You can now determine the values of $m$ and $b$ by substituting two points from the table of values.
  The following linear function yields the gasoline consumption for a given number of travelled kilometers:
  $\displaystyle f(x)\ =\ 0.075\cdot x$
  When is the fuel supply empty?
  The tank holds 56 liters of gasoline. You may now insert this value as $f (x)$ and calculate the associated $x$ -value:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rll} 56 &=& 0{.}075\cdot x \qquad \vert\ \colon 0{.}075 \\ 746{.}667 &=& x \end{array}$
  So the fuel will run out after about 746 km.
  When should the car be refueled?
  The car should be refueled, when there are 5 liters of gasoline in the tank. Since at the beginning, the tank holds 56 liters, the car will cosume exactly 51 liters until this point. You can insert this into the function just as above:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rll} 51 &=& 0{.}075\cdot x \qquad \vert\ \colon 0{.}075 \\ 680 &=& x \end{array}$
  So the car should be refueled after 680 km.
  Do you have a question?
  Write it here 👉
3
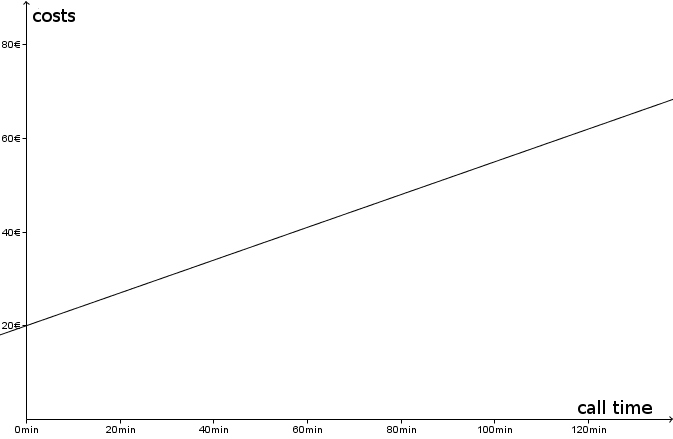
Mr. Smith has concluded a cell phone contract with the following conditions:
Monthly basic fee 20€, telephone costs per minute 0.35€.
1. How much is his monthly bill if he makes 40, 80 or 120 minutes of calls?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  Basic fee: 20€
  Costs per minute: 0.35€
  The monthly bill is given by taking the basic charge and adding the cost for the called minutes.
  Monthly bill for 40 minutes
  Mr. Smith was on the phone for 40 minutes.
  Calculate the cost for these 40 minutes.
  $40\cdot0.35€=14€$
  Add them to the basic fee.
  Monthly costs = $20 € + 14 € = 34 €$
  Mr. Smith pays 34€ if he calls for 40 minutes.
  Monthly bill for 80 minutes
  Mr. Smith was on the phone for 80 minutes.
  Calculate the cost for these 80 minutes.
  $80\cdot0.35€=28€$
  Add them to the basic fee.
  Monthly costs = $20 € + 28 € = 48 €$
  Mr. Smith pays 48€ if he calls for 80 minutes.
  Monthly bill for 120 minutes
  Mr. Smith was on the phone for 120 minutes.
  Calculate the cost for these 120 minutes.
  $120\cdot0.35€=42€$
  Add them to the basic fee.
  Monthly costs = $20 € + 42 € = 62 €$
  Mr. Smith pays 62€ if he calls for 120 minutes.
  Do you have a question?
  Write it here 👉
2. Create a function for the monthly cost depending on the call duration in minutes.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  Monthly cost = basic fee + cost of minutes called.
  Let $x$ be the number of minutes called.
  Use it to calculate the cost.
  Costs = $20€+0.35€\cdot x$
  Express this by a linear function.
  $f(x)=0.35\cdot x+20$
  Do you have a question?
  Write it here 👉
3. Visualize the relation (costs depending on call duration) graphically.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  $f (x) = 0.35 x + 20$
  This function has $y$ -axis intercept 20, so it intersects the $y$ -axis at $(0 ∣ 20)$ . Its slope is 0.35. So draw a point, e.g., at $(10\;|\;20+10\cdot0.35)=(10\,|\,23.5)$ . Connect these points by a line. This gives you the desired graph.
  Do you have a question?
  Write it here 👉

a	1 LU	2 LU	3 LU	4 LU	5 LU
$A_\square$	1 AU	4 AU	9 AU	16 AU	25 AU

distance traveled	0 km	100 km	200 km	300 km	400 km	500 km	600 km
fuel consumption	0 l	7.5 l	15 l	22.5 l	30 l	37.5 l	45 l

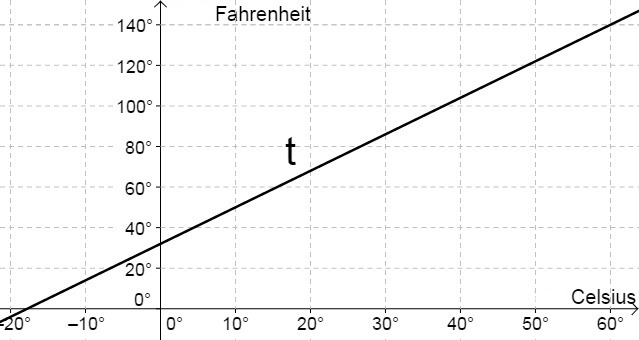
The following table gives the value in degrees Celsius (°C) and degrees Fahrenheit (°F) for some temperatures.

temperature (°C)	temperature (°F)
-10	14
0	32
20	68
60	140

This is a linear relation.

Draw the graph corresponding to this relation (Celsius on the $x$ -axis, Fahrenheit on the $y$ -axis) and give a function to convert a given Celsius temperature into a Fahrenheit temperature.

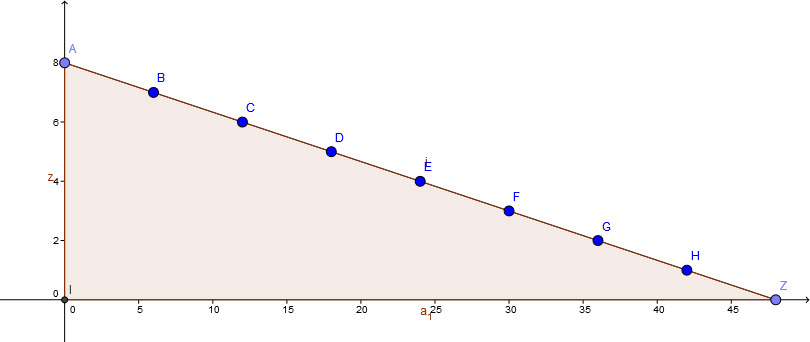
A delivery truck with a total load of $1.2\;t$ transports $x$ boxes of $25\;kg$ each and $y$ boxes of $150\;kg$ each.

Plot the relation between $x$ and $y$ on a graph, if only the total load is known.
Which points $\left(x|y\right)$ within the $x$ - $y$ -diagram are feasible, if you only know that the truck is loaded with at most $1.2 t$ ?

6
A magazine that can be purchased at a price of 2.20 € has a circulation of 120,000 copies. The publisher hired some market researchers who found out that the circulation can be increased by 5000 copies if the price is reduced by 0.20 € per magazine. Conversely, if the price is increased by 0.20 €, one loses 5000 buyers.
1. Calculate the price per magazine that would be necessary for a circulation of 140,000 copies.
  
  For an increase to 140,000 copies, determine by how much the circulation has changed:
  $\Delta N=140\,000-120\;000=20\,000$
  Determine the price change per additional copy $a$ from the problem definition: For 5000 additional copies, the price change is -0.2 €, so
  $a=\frac{\Delta p}{\Delta N}=\frac{-0.2}{5000}=-0.00004$
  Use this rate to determine the price change induced by $\Delta N$ copies.
  $\Delta p = a\cdot \Delta N=-0.00004\cdot 20\, 000=-0.8$
  Use this to calculate the new price.
  $p_{\mathrm{new}}=p_{\mathrm{old}}+\Delta p=2.2-0.8=1.4$
  So, with a circulation of 140,000 copies, the price is 1.40 € per copy.
  Do you have a question?
  Write it here 👉
2. What circulation can the publisher expect if it lowers the price of the magazine to 1.50 €?
  
  Suppose, the price has fallen to 1.50 €. The price change then is:
  $\Delta p=p_{\mathrm{new}}-p_{\mathrm{old}}=1.5-2.2=-0.7$
  Determine the number $b$ of additional copies per increase of the price by 1 €. (This is the inverse of the number $a$ in the first exercise part.)
  $a=\frac{\Delta N}{\Delta p}=\frac{-5000}{0.2}=-25\,000$
  Use this rate to determine the change of the circulation.
  $\Delta N=a\cdot \Delta p=(-25\,000) \cdot (-0.7)=17\,500$
  Determine the new circulation.
  $N_{neu}=N_{alt}+\Delta N=120\,000+17\,500=137\,500$
  So with a price of 1.50 € per copy, the circulation will be at 137,500 copies.
  Do you have a question?
  Write it here 👉
7
It is a very slow, completely undramatic "breakup history", step by step: The Eurasian continental plate moves away from the North American plate by two centimeters per year. If one were to follow the course of Columbus today, who sailed from Andalusia to the New World, one would have to cover about ___ meters more distance. That's hardly likely to upset a modern-day captain on the more than 6,000-kilometer voyage between Europe and America.
1. By how many meters has the distance increased?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  Hint: Columbus discovered America in 1492.
  This solution refers to the year 2022 and may need to be adjusted, if you are reading it later. First, we calculate the time that has passed since the discovery of America in 1492:
  $2022 - 1492 = 530$
  Computethe distance in centimeters
  $2\,\text{cm}\cdot530=1060\,\text{cm}$
  Convert cm into m.
  $1060\,\text{cm}\cdot10^{-2}=10.6\,\text{m}$
  The distance has already increased by 10.6 m since America was discovered.
  Do you have a question?
  Write it here 👉
2. How many years have to pass until another 5 meters of distance will have been added between the continental plates?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  Convert m in cm.
  $5.00\,\text{m}\cdot10^2=500\,\text{cm}$
  Determine the number of years.
  $500\,\text{cm}/2\,\text{cm}=250$
  It will take 250 years to add another 5.0 m of distance between the continental plates.
  Do you have a question?
  Write it here 👉
8
A patient receives an infusion. A full bottle contains 40 ml of infusion fluid. The drip rate is set such that 3 ml of the liquid passes through per minute. As soon as there is less than 5 ml in the bottle, it must be replaced. After how much time is this necessary?

Linear equations
At the beginning, you need to determine the maximum amount of infusion fluid that may drip out of the bottle before the replacement. For this, you need to subtract the 5 ml "safety buffer" from the 40 ml from the infusion bottle.
$40\text{ml}-5\text{ml}=35\text{ml}$
Now, determine the number of minutes until this amound of infusion has run out.
$\frac{35\text{ml}}{3\text{ml}}=\frac{35}{3}$
You may shorten the ml.
$\frac{35}{3}=11\frac{2}{3}$
The fraction in the end is converted into seconds.
$\frac{2}{3}\cdot60\text{sec}=40\text{sec}$
So in total, you get:
$11\text{min}+40\text{sec}=11\text{min}\,40\text{sec}$
The infusion bottle must be replaced after 11 minutes and 40 seconds at the latest.
9
Jonathan and Hannes decide to climb a very high mountain in the alps. Jonathan starts his hike at sea level (0m), while Hannes starts in a small shack at an altitude of (2500m).
Both may climb at 500m per hour. The function term describing Jonathan's ascent is
$j (x) = 500 x$
with $x$ denoting the time in hours. Decide which function term describes Hannes' ascent!
$h (x) = 500 x + 2500$
$h (x) = 2500 x$
$h (x) = 500 x - 2500$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Ascent of Hannes
To find the correct function term, you have to find the slope and the $y$ -axis intercept, given the values from the problem setting.
Since Jonathan and Hannes climb at the same speed, the function term of Hannes' ascent must have the same slope as the function term of Jonathan's ascent.
Jonathan's ascent is described with the function term $j (x) = 500 x$ .
Therefore, the slope of $j$ is 500.
The possible term $h (x) = 2500 x$ for Hannes' ascent is thereforeruled out. It would have a wrong slope!
Now two function terms with the correct slope but different $y$ -axis intercepts remain. Which of the terms is correct?
Compare the two $y$ -axis intercepts. These are $+ 2500$ and $- 2500$ .
You can quickly see that $+ 2500$ must be correct, because Hannes starts above Jonathan and therefore must be at the beginning $(x = 0)$ at $h (0) = 2500$ . By contrast, $h (0) = - 2500$ would mean that Hannes would start BELOW sea level, which does not make sense!
So you get a slope of 500 and a y-axis intercept of 2500.
The correct function term for Hannes' ascent is hence $h (x) = 500 x + 2500$ .
10
Max and Jana go on a trip to the game park "Oh My Deer" in Wild Brook. The entrance fee to the game park is $$ 5$ for two people. The game park offers the opportunity to buy special animal food for $$ 1$ at each enclosure to feed the animals.
(a) Determine how much Max and Jana have to spend for their trip if they want to buy either 5, 10 or 20 units of animal food in the game park. Create a table of values.
(b) Find a function $f (x)$ describing the costs of the trip in $$$ depending on the number $x$ of food units which Max and Jana buy.
(c) Visuallize the relationship from (b) by a plot of $f (x)$ .
(d) Max and Jana have $$ 14$ available at the beginning of their trip. Read off from the graph how much food they can buy.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
(a) If Max and Jana buy 5 units of food, they have to pay five times $$ 1$ in addition to the $$ 5$ entrance fee. So in total, they pay:
$\displaystyle \$5+5\cdot\$1=\$10$
If they buy 10 units of food, they have to pay in total
$\displaystyle \$5+10\cdot\$1=\$15$
For 20 units of food, the total costs are
$\displaystyle \$5+20\cdot\$1=\$25$
The table of values hence is:
Units of food
5
10
20
Total costs
$10
$15
$25
(b) If $x$ is the number of food units Max and Jana buy, then the two must pay $x$ dollars for the food. With the entrance fee of $5$ dollars, the total costs are given by
$\displaystyle f(x) = x + 5$
(c)
(d) To read off the number of units, start horizontally from the $y$ -axis at the total costs of $$ 14$ until you reach the function graph. This point corresponds to a trip with $$ 14$ spent.
From this point on the graph you go down vertically until you reach the $x$ -axis. In this case you end up at $x = 9$ . This is the number of food units Max and Jana have to buy in order to spend $$ 14$ in total.
So Max and Jana can buy up to 9 food units.
11
The National Aeronautics and Space Administration (NASA) is a huge space agency that can send rockets into space. For simplicity, we assume that a Rocket costs $\$500{,}000$ (real rockets are much more expensive). Before sending rockets into space, the NASA has to build a launchpad at the costs of $$ 1$ million.
(a) Calculate how much NASA spends in total when it launches 4, 6 or 10 rockets into space. Create a table of values from this.
(b) Set up a function that gives NASA's total costs $f (x)$ in $$$ million as a function of the number of rockets $x$ that are launched into space.
(c) Visualize the relationship from (b) by a plot.
(d) How many rockets can NASA send into space with a budget of $$ 10$ million.
12
At an altitude of 5000 m above Gloomington, dark clouds come up and it starts to rain. The raindrops fall down 500 m in one minute.
(Image source: https://pixnio.com/de/landschaften/regen/regentropfen-wasser#)
(a) Calculate the height of the raindrops above the ground after one, two and five minutes. Create a table of values from this.
(b) Find a function that gives the altitude $f (x)$ of the raindrops in m as a function of the elapsed time $x$ in minutes. (For simplicity, you can assume that there is no ground and the raindrops continue falling after reaching an altitude of 0m.)
(c) Visualize the relationship from (b) by a plot.
(d) How long does it take for the raindrops to reach the ground?
13
Maple Springs is known for its beautiful Indian summer: In the beginning of fall, the leaves of the trees turn yellow and red and start falling to the ground. Assume that a tree carries 12000 leaves in summer and starts to lose 1000 leaves every week, as fall begins.
(Image source: https://pixnio.com/de/landschaften/herbst/blaetter-im-herbst-gelblich-blaetter-rote-baeume-laub-herbst-herbst-blaetter-baeume)
(a) Set up a function for the number of leaves $f (x)$ on the tree as a function of the number of weeks $x$ that have passed since the beginning of fall.
(b) Draw this relationship in a coordinate system. Plot the number of leaves (in thousands) on the $y$ -axis and the number of elapsed weeks on the $x$ -axis.
(c) How many leaves are there on the tree after 1, 2, 3, 6 and 12 weeks, respectively?

Units of food	5	10	20
Total costs	$10	$15	$25

Water is filled into an empty Jacuzzi. Per minute, 40 liters of water flow into the Jacuzzi.

Complete the table:
Time (in min)
0
1
2
5
8.2
15
25
Water(in liters)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
At the beginning, the Jacuzzi is empty. So after 0 minutes there are 0 liters of water in the pool.
After 1 minute there are $1\cdot40=40$ liters of water in the Jacuzzi.
After 2 minutes there are $2\cdot40=80$ liters of water in the Jacuzzi.
After 5 minutes there are $5\cdot40=200$ liters in the Jacuzzi.
.......
and so on.
The completed table looks like this:
Time(in min)
0
1
2
5
8.2
15
25
Water(in liters)
0
40
80
200
328
600
1000
Do you have a question?
Write it here 👉
The function $f\left(x\right)$ is defined as the volume in the Jacuzzi (in liters) in dependence of the time $x$ (in minutes).
Draw the points of the function $f$ computed in (a) into a coordinate system and draw the graph of the function $f$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
The plot looks as follows:
Do you have a question?
Write it here 👉
What is the equation of this function $f (x)$ that gives the amount of water (in liters) as a function of time $x$ (in minutes)?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
$x$ : Time in minutes
$y$ : Amount of water in liters in the Jacuzzi
After $x$ minutes we have $y=x \cdot40$ liters in the Jacuzzi.
So the function we are looking for is $f(x)=40\cdot x$
Do you have a question?
Write it here 👉

Time(in min)	0	1	2	5	8.2	15	25
Water(in liters)	0	40	80	200	328	600	1000

The Jacuzzi holds 750 liters in total.

What does thin mean for the graph from (b)?

Read off and calculate after what time (in minutes) the water supply must be turned off, as the Jacuzzi is filled.

A candle is $18\; \text{cm}$ long before being lit. When burning, it becomes shorter by $1.5\; \text{cm}$ every hour.

How many hours does it take for the candle to burn down completely?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Each hour the candle gets shorter by $1.5\; \text{cm}$ . You get the burning time in hours by calculating how many times the $1.5\; \text{cm}$ is included in the total length of $18\; \text{cm}$ : $\frac{18}{1{,}5}=12$
Answer: After 12 hours the candle has burned down completely.
Do you have a question?
Write it here 👉
Draw the graph of the function $f$ describing the length $y$ (in $\text{cm}$ ) of the candle in terms of the burning time $x$ (in hours).

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Graph of $f$
To draw a linear function, you need two points that lie on the graph.
One point is given in the problem setting. At the beginning $x = 0$ the candle is $y = 18$ centimeters long, so $P\left(0 \vert 18\right)$ is a point on the graph.
In part a) you found out that the candle burs down after $x = 12$ hours , i.e. the candle length is then $0\; \text{cm}$ . So $Q\left(12 \vert 0\right)$ also lies on the graph.
Draw the two points in a coordinate system and connect them.
Do you have a question?
Write it here 👉
Find the equation of $f$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
Finding the function equation
Examples of the candle length $y$ after a certain burning time $x$ :
At the beginning, $\textcolor{006400}{y}=18$ .
After $\textcolor{ff6600}{1}$ hour, the length of the candle in $\text{cm}$ is:
$\displaystyle \textcolor{006400}{y}=18 -1.5 \cdot \textcolor{ff6600}{1}=16.5$
After $\textcolor{ff6600}{2}$ hours, the length of the candle in $\text{cm}$ is:
$\displaystyle \textcolor{006400}{y}=18-1.5\cdot\textcolor{ff6600}{2}=15$
After $\textcolor{ff6600}{x}$ hours, the length of the candle in $\text{cm}$ is:
$\displaystyle \textcolor{006400}{y} = 18-1.5\cdot \textcolor{ff6600}{x}$
So the function equation is $y=-1.5\cdot x+18$
Answer: The equation describing the length of the candle as a function of time is:
$\displaystyle y=-1.5\cdot x+18$
Do you have a question?
Write it here 👉

Calculate the length of the candle after 5 or 8 hours. Check your calculated values using the graph.

Calculate after how many hours, only $3 \; \text{cm}$ of the candle are remaining.

16
A water supplier charges 1.50 € per $m^{3}$ of water (consumption costs).
In addition, the customer must pay a monthly basic fee of 6 € for maintenance work carried by the supplier.
1. Complete the table.
  Water consumption(in m³)
  0
  1
  2
  3
  7,8
  15
  20
  Consumption costs (in €)
  Total costs (in €)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  You calculate the total cost as the sum of the water consumption cost per $m^{3}$ and the basic fee. (Even if no water is consumed, the basic fee must be paid).
  0 $\text{m}^3$ cost $0\;\cdot 1.50 \;\text{€}$ plus the basic fee of 6 € $\;\Rightarrow$ Total costs: $y = 0\;\cdot 1.50 \;\text{€}+6\;\text{€}=6\;\text{€}$
  1 $\text{m}^3$ costs $0\;\cdot 1.50 \;\text{€}$ plus the basic fee of 6 € $\;\Rightarrow$ Total costs: $y = 1\;\cdot 1.50 \;\text{€}+6\;\text{€}=7.50 \;\text{€}$
  2 $\text{m}^3$ cost $0\;\cdot 1.50 \;\text{€}$ plus the basic fee of 6 € $\;\Rightarrow$ Total costs: $y = 2\;\cdot 1.50 \;\text{€}+6\;\text{€}=9 \;\text{€}$
  Accordingly, you calculate the other values in the table.
  The complete table looks like this:
  Water consumption(in m³)
  0
  1
  2
  3
  7,8
  15
  20
  Consumption costs(in €)
  0
  1.50
  3.00
  4.50
  11.70
  22.50
  30.00
  Total costs (in €)
  6.00
  7.50
  9.00
  10.50
  17.70
  28.50
  36.00
  Do you have a question?
  Write it here 👉
2. Draw the graph of the function $f$ describing the total monthly bill $y$ (in €) in terms of the water consumption $x$ (in $m^{3}$ ).
  Also determine the equation of $f$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linear function
  Drawing the graph of $f$
  From the table you can take the coordinates of 2 points, e.g. $P(0\vert 6)$ and $Q(2\vert 9)$ .
  Draw the two points in a coordinate system and connect them with a half line starting at point $P$ .
  Note: There is no negative water consumption. Therefore, the graph of the function $f$ starts at the point $P$ .
  Determining of the function equation:
  1 $\text{m}^3$ water costs $1\;\cdot 1.50 \;\text{€}$ plus the basic fee of 6 € $\;\Rightarrow$ Total costs: $y = 1\;\cdot 1.50 \;\text{€}+6\;\text{€}$
  2 $\text{m}^3$ cost $2\;\cdot 1.50 \;\text{€}$ plus the basic fee of 6 € $\;\Rightarrow$ Total costs: $y = 2\;\cdot 1.50 \;\text{€}+6\;\text{€}$
  ........
  $x$ $\text{m}^3$ cost $x\;\cdot 1.50 \;\text{€}$ plus the basic fee of 6 € $\;\Rightarrow$ Total costs: $y = x\;\cdot 1.50 \;\text{€}+6\;\text{€}$
  These considerations lead you to the function equation: $y=1.5\cdot x+6$
  Answer: The function equation is: $y=1.5\cdot x+6$
  Do you have a question?
  Write it here 👉

Water consumption(in m³)	0	1	2	3	7,8	15	20
Consumption costs(in €)	0	1.50	3.00	4.50	11.70	22.50	30.00
Total costs (in €)	6.00	7.50	9.00	10.50	17.70	28.50	36.00

This content is licensed under
CC BY-SA 4.0 → Info

$\displaystyle m_t$	$=$	$\displaystyle \frac{y_B-y_A}{x_B-x_A}$
	↓	Plug in the values.
$\displaystyle m_t$	$=$	$\displaystyle \frac{68-32}{20-0}=1.8$

$\displaystyle x\cdot25+y\cdot150$	$=$	$\displaystyle 1200$	$\displaystyle -x\cdot25$
	↓	Rearrange the equation so that you get a line equation.
$\displaystyle 150\cdot y$	$=$	$\displaystyle -25\cdot x+1200$	$\displaystyle :150$
$\displaystyle y$	$=$	$\displaystyle -\frac{25}{150}\cdot x+\frac{1200}{150}$
	↓	Shorten the fractions.
$\displaystyle y$	$=$	$\displaystyle -\frac{1}{6}\cdot x+8$

$\displaystyle y$	$=$	$\displaystyle 40\cdot x$
	↓	$y = 750$
$\displaystyle 750$	$=$	$\displaystyle 40\ \cdot\ x$	$\displaystyle :40$
	↓	Solve for $x$ .
$\displaystyle x$	$=$	$\displaystyle \frac{750}{40}$
	$=$	$\displaystyle 18.75$

$\displaystyle y$	$=$	$\displaystyle 18-1.5\cdot\ x$
	↓	plug in $x = 5$
	$=$	$\displaystyle 18-1.5\cdot5$
	$=$	$\displaystyle 18-7.5$
	$=$	$\displaystyle 10.5$

$\displaystyle y$	$=$	$\displaystyle 18-1.5\cdot\ x$
	↓	Plug in $x = 8$
	$=$	$\displaystyle 18-1.5\cdot\ 8$
	$=$	$\displaystyle 18-12$
	$=$	$\displaystyle 6$

$\displaystyle y$	$=$	$\displaystyle 18-1.5\cdot\ x$
	↓	plug in $y = 3$
$\displaystyle 3$	$=$	$\displaystyle 18-1.5\ \cdot\ x$	$\displaystyle +1.5\ \cdot\ x$
	↓	Shift terms with $x$ to the left.
$\displaystyle 3+1.5\cdot\ x$	$=$	$\displaystyle 18$	$\displaystyle -3$
	↓	Shift numbers to the right.
$\displaystyle 1.5\ \cdot\ x$	$=$	$\displaystyle 15$	$\displaystyle :1.5$
$\displaystyle x$	$=$	$\displaystyle \frac{15}{1.5}$
	$=$	$\displaystyle 10$

Applied exercises: Linear functions

Example

Do you have a question?

Example

Do you have a question?

Example

Do you have a question?

Example

Do you have a question?

Example

Do you have a question?

Example

Do you have a question?

Example

Do you have a question?

Example

Do you have a question?

Do you have a question?

Do you have a question?

When is the fuel supply empty?

When should the car be refueled?

Do you have a question?

Monthly bill for 40 minutes

Monthly bill for 80 minutes

Monthly bill for 120 minutes

Do you have a question?

Do you have a question?

Do you have a question?

Part 1

Plot within a diagram

Part 2

Do you have a question?

Do you have a question?

Do you have a question?

Do you have a question?

Linear equations

Ascent of Hannes

To find the correct function term, you have to find the slope and the yyy-axis intercept, given the values from the problem setting.

Since Jonathan and Hannes climb at the same speed, the function term of Hannes' ascent must have the same slope as the function term of Jonathan's ascent.

Jonathan's ascent is described with the function term j(x)=500xj(x)=500xj(x)=500x.

Therefore, the slope of jjj is 500.

The possible term h(x)=2500xh(x)=2500xh(x)=2500x for Hannes' ascent is thereforeruled out. It would have a wrong slope!

Now two function terms with the correct slope but different yyy-axis intercepts remain. Which of the terms is correct?

Compare the two yyy-axis intercepts. These are +2500+2500+2500 and −2500-2500−2500.

So you get a slope of 500 and a y-axis intercept of 2500.

The correct function term for Hannes' ascent is hence h(x)=500x+2500h(x)=500x+2500h(x)=500x+2500.

Do you have a question?

Do you have a question?

Do you have a question?

Adapting the function graph

Calculation of the time until the Jacuzzi is filled:

Do you have a question?

Do you have a question?

Graph of fff

Do you have a question?

Finding the function equation

Do you have a question?

Plug x=5x=5x=5 into the function equation.

Plug x=5 into the function equation.

Do you have a question?

Plug y=3y = 3y=3 into the function equation and solve for xxx.

Do you have a question?

Do you have a question?

Drawing the graph of fff

Determining of the function equation:

Do you have a question?

To find the correct function term, you have to find the slope and the $y$ -axis intercept, given the values from the problem setting.

Jonathan's ascent is described with the function term $j (x) = 500 x$ .

Therefore, the slope of $j$ is 500.

The possible term $h (x) = 2500 x$ for Hannes' ascent is thereforeruled out. It would have a wrong slope!

Now two function terms with the correct slope but different $y$ -axis intercepts remain. Which of the terms is correct?

Compare the two $y$ -axis intercepts. These are $+ 2500$ and $- 2500$ .

The correct function term for Hannes' ascent is hence $h (x) = 500 x + 2500$ .

Graph of $f$

Plug $x = 5$ into the function equation.

Plug $y = 3$ into the function equation and solve for $x$ .

Drawing the graph of $f$