Exercises: Intersection of two lines
- 1
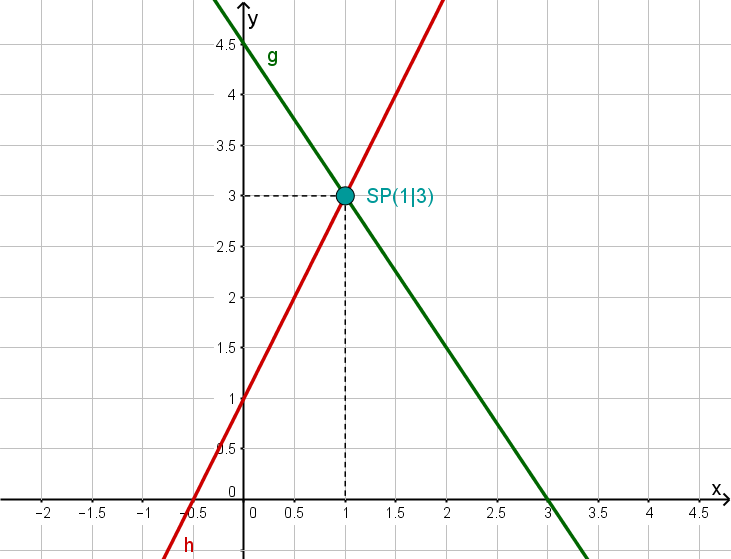
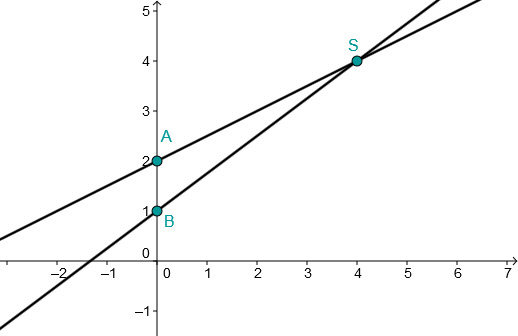
Bestimme den Schnittpunkt beider Geraden und zeichne diesen in ein Koordinatensystem.
For this task you need the following basic knowledge: Linear function
Set the functions and equal to obtain the intersection point.
↓ add
Insert into one of the two lines equations, for example :
↓ subtract
Sketch
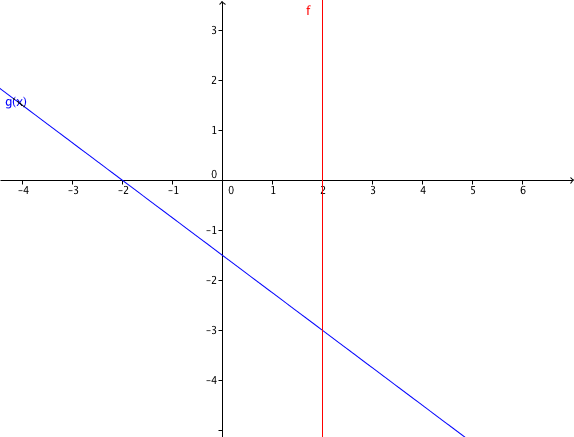
For this task you need the following basic knowledge: Linear function
Set the functions and equal to obtain the intersection point.
First solve the function for .
Now set f and g equal
↓ add and subtract
Plug into one of the two line equations, for example :
↓ add
- 2
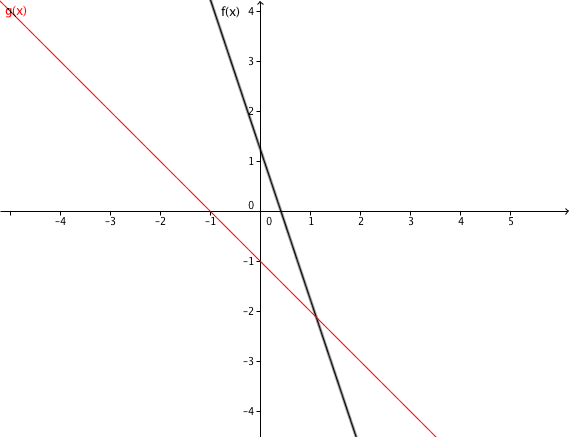
Determine the intersection of the two lines and draw the graphs in a coordinate system.
For this task you need the following basic knowledge: Linear function
Determining the intersection point
Set and equal.
↓ Subtrahiere und vertausche die Seiten.
↓ Plug x into one of the two function equations.
is the intersection point.
Sketch
Connect the -axis intercepts (here and ) with the calculated intersection point to obtain the lines.

- 3
Calculate the intersection points of a straight line.
Consider are the function equations of the two lines and . Calculate the intersection of the two lines and draw the lines in a coordinate system.
For this task you need the following basic knowledge: Linear function
Calculating the line intersection
Set and equal.
↓ Plug into .
Sketch
Connect the -axis intercepts (here and ) with the calculated intersection point . This way you obtain the two lines.
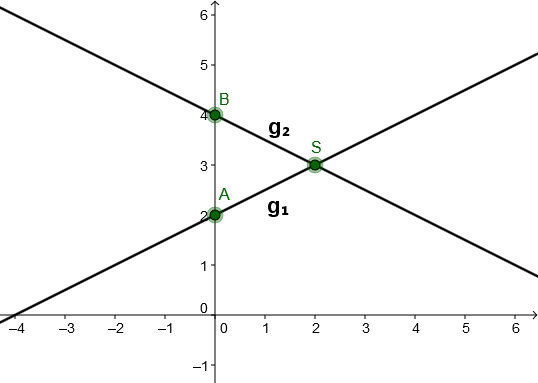
For this task you need the following basic knowledge: Linear function
Calculating the line intersection
Set and equal.
↓ Plug into .
Sketch
Connect the -axis intercepts (here and ) with the calculated intersection point . This way you obtain the two lines.

For this task you need the following basic knowledge: Linear function
Calculating the line intersection
Set and equal.
↓ Plug into .
Sketch
Connect the -axis intercepts (here and ) with the calculated intersection point . This way you obtain the two lines.
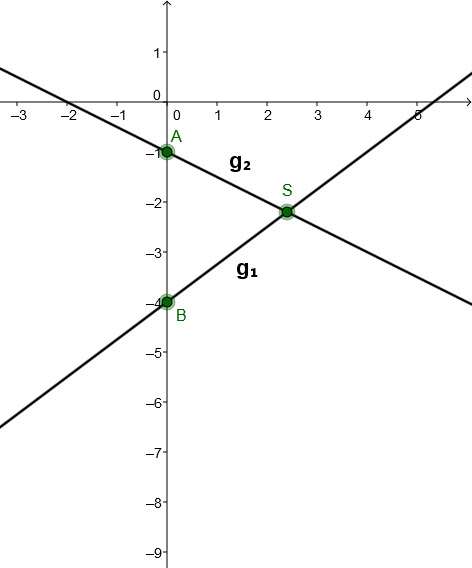
For this task you need the following basic knowledge: Linear function
Calculating the line intersection
Set and equal.
↓ Plug into .
Sketch
Connect the -axis intercepts (here and ) with the calculated intersection point . This way you obtain the two lines.
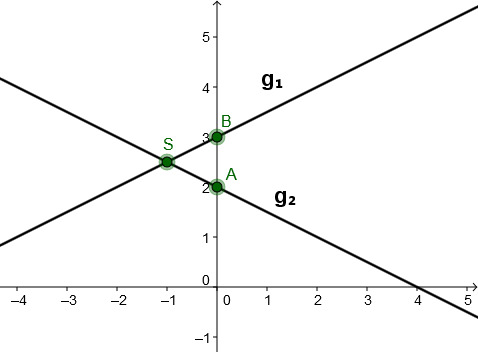
For this task you need the following basic knowledge: Linear function
Calculating the line intersection
Set and equal.
↓ Get the fractions on a common denominator.
↓ subtract
↓ dividing by a fraction multiplying with the inverse
↓ Plug into .
↓ Sketch
Connect the -axis intercepts (here and ) with the calculated intersection point . This way you obtain the two lines.
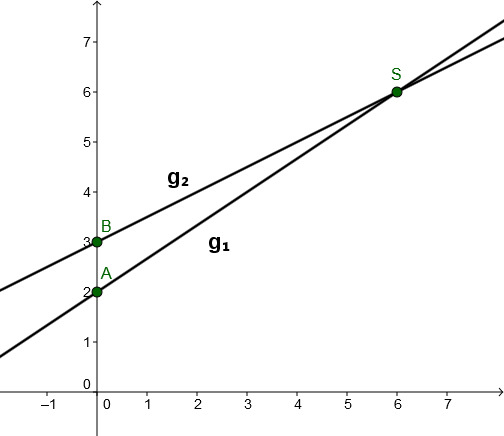
For this task you need the following basic knowledge: Linear function
Calculating the line intersection
Set and equal.
Sketch
Connect the -axis intercepts (here and ) with the calculated intersection point . This way you obtain the two lines.
- 4
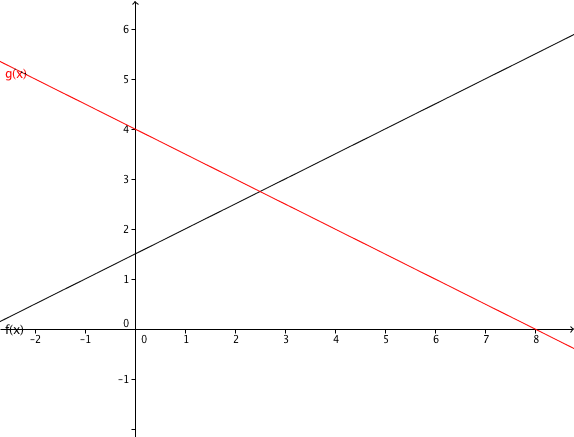
Consider the following graphs.
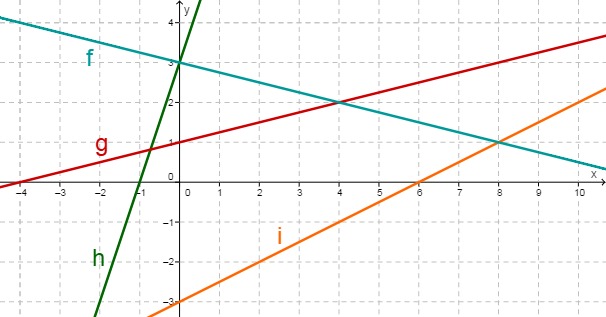
Determine the function equations of all 4 lines.
For this task you need the following basic knowledge: Line equation
Line equation of
In order to determine the line equation of , first read off two points from the diagram that lie on the straight line . In the above example, you may for instance get and . Use these two points to determine the slope of via the difference quotient
Plug in the values
Now determine the -axis intercept by plugging in any point on into the general line equation. Alternatively, you may directly read off at which value intersects the -axis (if possible).
For instance, plug in .
Simplify.
So the line equation is .
Line equation of
In order to determine the line equation of , first read off two points from the diagram that lie on the straight line . In the above example, you may for instance get and . Use these two points to determine the slope of via the difference quotient
Plug in the values
Now determine the -axis intercept by plugging in any point on into the general line equation. Alternatively, you may directly read off at which value intersects the -axis (if possible).
For instance, plug in .
Simplify.
So the line equation is .
Line equation of
In order to determine the line equation of , first read off two points from the diagram that lie on the straight line . In the above example, you may for instance get and . Use these two points to determine the slope of via the difference quotient
Plug in the values
Now determine the -axis intercept by plugging in any point on into the general line equation. Alternatively, you may directly read off at which value intersects the -axis (if possible).
For instance, plug in .
Simplify.
So the line equation is .
Line equation of
In order to determine the line equation of , first read off two points from the diagram that lie on the straight line . In the above example, you may for instance get and . Use these two points to determine the slope of via the difference quotient
Plug in the values
Now determine the -axis intercept by plugging in any point on into the general line equation. Alternatively, you may directly read off at which value intersects the -axis (if possible).
For instance, plug in .
Simplify.
So the line equation is .
Determine the intersection of g and h , and the zero of f.
Intersection point of and
To determine the point of intersection of two functions, you set them equal and solve for . The function equations (determined in the previous problem) are and .
↓ subtract and .
↓ divide by .
Now substitute into the line equation of or to determine .
Plug in .
The lines and therefore intersect at .
You may obtain the zero of by setting the function equation equal to 0 and solving for .
So has the zero 12.
Calculate the two intersections that lie outside the figure.
The intersection of and and the intersection of and lie outside the figure above.
Intersection point of and
To determine the point of intersection of two functions, you set them equal and solve for . The function equations (determined in the previous problem) are and .
Now substitute into the line equation of or to determine .
Plug in .
The lines and therefore intersect at .
Intersection point of and
To determine the point of intersection of two functions, you set them equal and solve for . The function equations (determined in the previous problem) are and .
Now substitute into the line equation of or to determine .
Plug in .
The lines and therefore intersect at .
What is the maximum number of intersections of four straight lines?
If no pair of lines is parallel, then there are a total of 6 intersections, namely the following:
and
and
and
and
and
and
- 5
Calculate the intersection of the pairs of lines.
and
↓ The functions are set equal to calculate the -coordinate of the intersection.
↓ Insert the -value into one of the two functions to calculate the -coordinate
↓ First multiply, then divide.
↓ Intersection point:
and
↓ The functions are set equal to calculate the -coordinate of the intersection.
↓ Insert the -value into one of the two functions to calculate the -coordinate
↓ First multiply, then divide.
↓ Intersection point:
and
↓ The functions are set equal to calculate the -coordinate of the intersection.
↓ Insert the -value into one of the two functions to calculate the -coordinate
↓ First multiply, then divide.
↓ Intersection point:
and
Geraden mit gleicher Steigung (hier 7) schneiden sich nicht, denn sie sind parallel zueinander.Setzt man die Funktionsterme gleich, so erhält man eine falsche Aussage, also keinen Schnittpunkt.
↓ False statement!
and
↓ The functions are set equal to calculate the -coordinate of the intersection.
↓ Insert the -value into one of the two functions to calculate the -coordinate
↓ First multiply, then divide.
↓ Intersection point:
and
↓ The functions are set equal to calculate the -coordinate of the intersection.
↓ Insert the -value into one of the two functions to calculate the -coordinate
↓ Intersection point:
- 6
Show by calculation that the three straight lines ; and intersect at exactly one point.
: ; :
Es ist hier zu empfehlen, zunächst den Schnittpunkt von zwei Geraden zu berechnen und dann zu prüfen, ob der Schnittpunkt auch ein Punkt auf der anderen Gerade ist.
Zwei der drei Geraden werden gleichgesetzt um die x-Koordinate des Schnittpunktes zu berechnen.
↓ First add 2x and then 1.5.
↓ divide by 3.
Insert the -value into one of the two line equations (e.g. that of ) to calculate the -coordinate of the intersection of and .
Now check whetehr the intersection point is also in the third line:
:
The point of intersection is now inserted into . This means that and of the are replaced by 3 and 1.5.
Check whether the resulting statement is true in order to determine whether runs through .
This is a true statement, so is the common and only intersection of all three straight lines.
- 7
Check whether the following lines and run through a common point.
For this task you need the following basic knowledge: Linear function
First bring all lines equations into the general form .
Line :
Line :
Line :
Determine the intersection of and
Set the respective right sides equal.
↓ Get all -terms on one side.
↓ Conclude
↓ Plug into to get the -coordinate.
The intersection point is
Determine the intersection of and
Set the respective right sides equal.
↓ Get all -terms on one side.
↓ Conclude.
↓ Plug into to get the -coordinate.
The intersection point is
Since intersects with and with at the same point, and also intersect at this point.
The lines therefore all run through the common point .
For this task you need the following basic knowledge: Linear function
First bring all lines equations into the general form .
Line :
Line :
Line :
Determine the intersection of and
Set the respective right sides equal.
↓ Get all -terms on one side.
↓ Conclude.
↓ Plug into to get the -coordinate.
The intersection point is
Determine the intersection of and
Set the respective right sides equal.
↓ Get all -terms on one side.
↓ Conclude.
↓ Plug into to get the -coordinate.
The intersection point is
Thus the line intersects the line at a different point than the line . So the lines do not run through a common point.
- 8
Determination of intersection points
Consider the following two lines and .
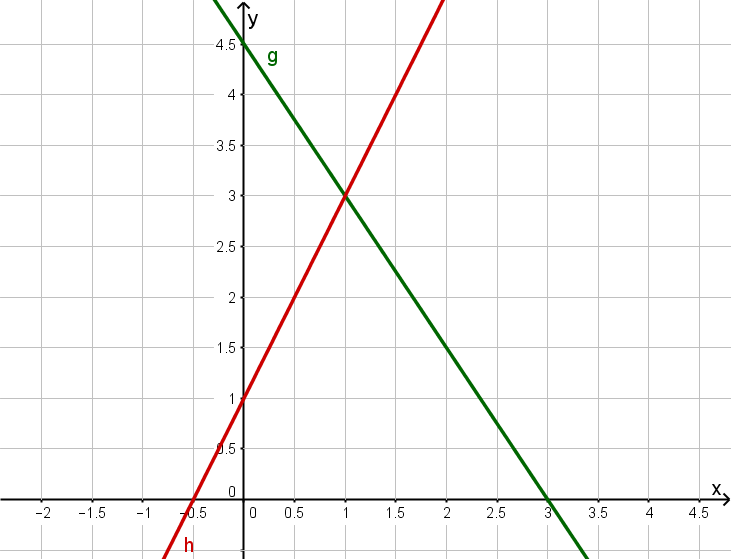
Determine the line equations of and .
For this task you need the following basic knowledge: Line equation
The parameter is the slope of the line. The parameter is the -axis intercept.
Line :
The line has slope , so .
It intersects the -axis at , so .
Line :
The line has slope , so
It intersects the -axis at , so .
Read off the intersection point.
For this task you need the following basic knowledge: Lines in coordinate systems
Reading off the intersection point
From the plot, we may read off the intersection point .